Algorithm - Disjoint Set

Disjoint Set 顧名思義，代表了一群兩兩交集為空的集合們，常用於處理依據某種關係將元素們「分類」的問題。我們的目標是去 maintain collection of disjoint sets $S_1,S_2,\cdots,S_k$，而每個 $S_i$ (每個 category) 以一個代表值 (representative) 去紀錄。

支援的 Operations

1. Make-Set(x): create a new set {$x$}
2. Find(x): Find the leader of $x$’s set
3. Union(x,y): Union $x$’s set and $y$’s set

Linked List Implementation

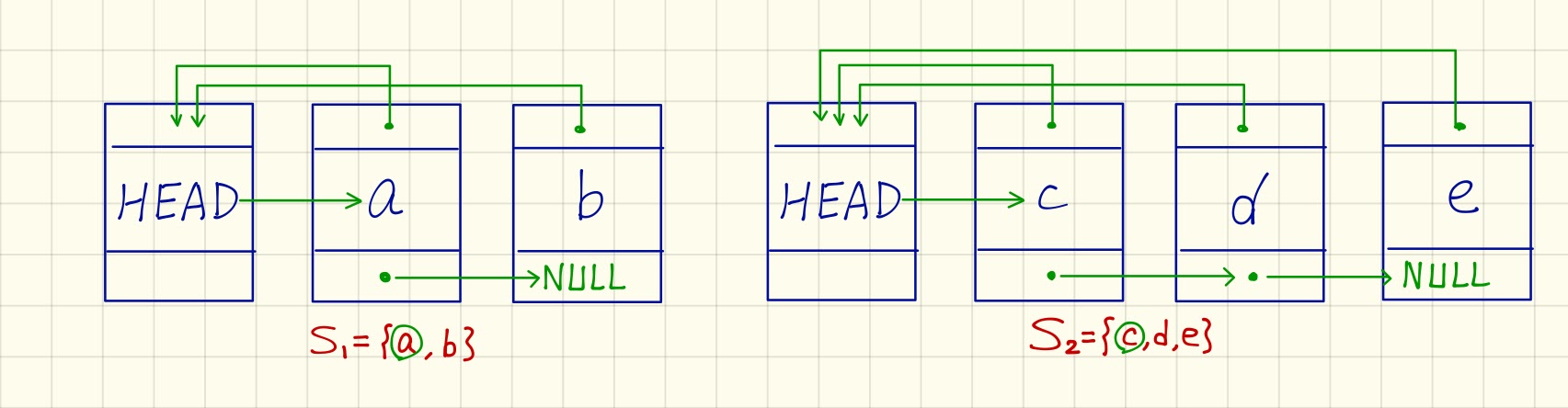
• Make-Set(x): $\mathcal{O}(1)$ (create HEAD and representative，也就是自己)
• Find(x): $\mathcal{O}(1)$ (back to HEAD，go to representative)
• Union(x,y): $\mathcal{O}(n)$
  可以發現 Union 非常慢，要依序將 $S_2$ 中的元素依序指到 $S_1$ 的 HEAD ，同時將 $S_1$ 的最後一個元素之 ptr 指到原先 $S_2$ 中的第一個。(當然可以在 HEAD 中多存一個指向最後一個元素的 ptr ，但複雜度還是 $\mathcal{O}(m)$, where $m = |S_2|$)

雖說單看 Union 的複雜度似乎不太妙，但考慮一系列操作( Amortized Analysis ，也是一種常見的分析複雜度方式)，同時利用上方提到的 trick ，在做 Union 時，都是去合併較小的那個集合，再來做分析。

Lemma

Starting from 0 sets

$\Rightarrow \, \text{total cost}: \mathcal{O}(m+n \log n)$
其中 $n\log n$ 顯然是來自 Union 的 cost，而細看操作會發現，這亦為 $\mathcal{\Theta}(\text{total number of times that element’s top ptr changes})$，
所以今天我們想證明，改動 ptr 的次數為 $\mathcal{O}(n \log n)$

Claim: If an element has changes ptr $k$ times, then it belongs to a set of size $\geq 2^{k}$

用數學歸納法可以簡單證明，假設 $k=t$ 時成立，那在 $k=t+1$ 時，如果該 set 還需改動 ptr ，表示其跟 size 比他大的 set 做 Union ，之後 size $\geq 2^{t+1}$ ， Claim 依然成立 ($k=0$ 時，只有 make-set， size 為 $1$ 亦成立)

而利用該 Claim ，又已知 size of any set $\leq n$，所以任何元素都只能改動 ptr $\leq \log n$ 次，所以 total ptr 改動次數 $\leq n \log n \quad \square$

Forest Implementation

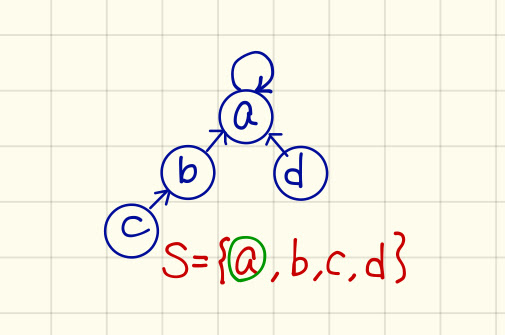
• Make-Set(x): $\mathcal{O}(1)$ (建一顆只有一個節點的樹，root指向自己)
• Find(x): $\mathcal{O}(\text{height})$ (trace back to root)
• Union(x,y): $\mathcal{O}(\text{height})$ (單純改變被合併集 root 的指向為 $\mathcal{O}(1)$ ，但要先用 Find 找到 root)

稍微觀察一下發現，如果今天這個樹長的很傾斜(最爛的情況就是 skewed tree ，直接退化成 list)，那麼 height 為 $\mathcal{O}(n)$ ，複雜度沒有任何改進。但若仿效前面 linked list 的想法，在做 Union 時，去合併比較小的 set ，則可以避免這個問題 (skewed tree會發生，就是每次都是拿一個 size 非 $1$ 的 set 去接在 size 為 $1$ 的 set 後面…)。

Theorem: The height of every tree $\leq \log n$

Claim: every tree with height $k$ has at least $2^{k-1}$ elements

• $k=1$, trivial
• 假設 $k=t$ 成立，考慮兩個高度同為 $t$ 的樹(如果不一樣的話，那合併後的樹高度為原先兩者中較高的那個，但元素個數又增加了，Claim 必成立)，各自至少有 $2^{t-1}$ 個元素，合併後高度變為 $t+1$ ，元素個數 $\geq 2^{t-1} \times 2 = 2^{t}$， Claim 依然成立

所以當已知每顆樹至多 $n$ 個元素的情況下，我們可以證明其高度必 $\leq \log n \quad \square$

Implementation

Reference

• 台大資工 - DSA