Advanced Algorithm - Metric Facility Location Revisited

3-Approx. Algorithm (Primal-Dual method)

Advanced Algorithm
Algorithm / Linear Programming / Approximation Algorithm / NTU

前面提到過一個較為複雜的優化問題， Metric Facility Location Problem ，並給出了一個 4-Approx. Algorithm ，於這講中，我們要來利用前面提到的 Primal-Dual method 來設計演算法。

Rewrite Dual form

Primal LP

$$ \min \sum_{i \in F}y_i f_i + \sum_{i \in F, \, j \in C} x_{ij} c_{ij} \; s.t. \, \begin{cases} \sum_{i \in F}x_{ij} \geq 1, \; \forall j \in C \; (\text{乘上} \, \color{red}{\alpha_j})\\ y_i \geq x_{ij}, \; \forall i \in F, \, j \in C \; (\text{乘上} \, \color{green}{\beta_{ij}})\\ x_{ij}, \, y_i \geq 0 \end{cases} $$

Dual LP

$$ \min \sum_{j \in C} \color{red}{\alpha_j} \; s.t. \, \begin{cases} \sum_{j \in C} \color{green}{\beta_{ij}} \leq f_i \; \forall i \in F \, (y_i \, \text{的 objective}) \\ \color{red}{\alpha_j} - \color{green}{\beta_{ij}} \leq c_{ij} \; \forall i \in F, j \in C \, (x_{ij} \, \text{的 objective}) \\ \alpha_j ,\beta_{ij} \geq 0 \end{cases} $$

對於 Dual var 的直觀理解

把 $\alpha_j$ 想成是 clinet $j$ 所付的錢，而 $\beta \scriptstyle ij$ 表示其貢獻給 facility $i$ 的，先把原先條件中的不等式改為等式 (complementary slackness)，第一條式子，表示被開的 facility is fully paid for。而第二條式子，把 $\alpha_j$ 拆成兩部份，一部分給 facility ，另一部份則用於支付 $c \scriptstyle ij$ 的 coneection cost 。

Algorithm

Phase I (Increase $\alpha$ and $\beta$)

Initially, set $\alpha_i$ and $\beta \scriptstyle ij$ to $0 ; \forall i,j$

  1. Increase all uncovered $\alpha_j$ with same rate until $\alpha_i = c\scriptstyle ij$ for some $i,j$， call $\color{blue}{(i,j) , \text{is tight}}$

  2. When $(i,j)$ is tight, set $\beta \scriptstyle ij \normalsize = \alpha_j - c \scriptstyle ij$ (僅可能緩慢地讓 $\beta$ 隨 $\alpha$ increase ，在滿足第一條 constraint 的情況下，不要讓 $\alpha$ 的增長太快碰到第二條 constraint)

Repeat above procedure, until $\color{blue}{\underset{j \in C}{\sum}\beta \scriptstyle ij \normalsize = f_i , \text{for some} , i}$

Then, facility $i$ becomes temporarily opened，\
$\forall j$ such that $(i,j)$ is tight and $j$ is not covered, temporarily connect $j$ to $i$, 之後的 Phase I 中， $\alpha_j$ is fixed。 And we say $\color{blue}{\text{facility} , i , \text{is client} , j \text{‘s witness}}$

Repeat above procedure until all clients are covered

Remark: 如果在 facility $i$ 被開之後，有其他的 client $j^\prime$ 使其 connection 為 tight，我們也稱 facility $i$ 為 client $j^\prime$ 的 witness (Note: 往後 $\alpha \scriptstyle j^\prime$ 會 fixed ，且 $\beta \scriptstyle ij^\prime \normalsize = \alpha \scriptstyle j^\prime \normalsize - c \scriptstyle ij^\prime \normalsize = 0$**，不會再更動**)

Phase II (First remove all closed facilities and edges not tight)

Def.: if $\beta \scriptstyle ij \normalsize > 0$ and $\beta \scriptstyle ij^\prime \normalsize > 0$, we call $i, i^\prime$ are $\color{blue}{\text{conflict}}$

(clinet $j$ 同時有付錢給兩者，均有貢獻 $\beta \scriptstyle \star j$)

Pick any maximal set of temporarily opened facilities $\mathbf{I}$ that AREN'T conflicting

  1. open $\mathbf{I}$
  2. If client $j$'s witness $\in I$, connect directly
  3. If not, connect indirectly to any conflicting $i \in I$

Correctness

Complementary Slackness Revisited

  1. $\forall i \in F, , ; y_i = 0 \lor \underset{j \in C}{\sum} \beta \scriptstyle ij \normalsize = f_i$ \
    (對有開的 facility, $\sum \beta \scriptstyle ij \normalsize = f_i$) $\Rightarrow$ 符合！

  2. $\color{red}{\forall i \in F , j \in C, ; x \scriptstyle ij \normalsize = 0 \lor \alpha_j - \beta \scriptstyle ij \normalsize = c \scriptstyle ij}$

  3. $\forall j \in C, , ; \alpha_j = 0 \lor \underset{i \in F}{\sum} x \scriptstyle ij \normalsize = 1$\
    (對所有的 client 而言，其只會被一個 facility serve) $\Rightarrow$ 符合！

  4. $\forall i \in F, j \in C, , ; \beta \scriptstyle ij \normalsize = 0 \lor y_i = x \scriptstyle ij$\
    (對那些 directly connected 的 clinet，也就是 $\beta \scriptstyle ij \normalsize \not = 0$ 者，$j$ 是由 $i$ serve\
    但注意到為 $0$ 者也可能是被 directly connect 的) $\Rightarrow$ 符合！

Remark: 1,2 分別為一組， 3,4 為另一組 complementary slackness，而現在我們要 relax 第一組 3 倍 (因為對 indirectly connected 的那些 clinet ， $\color{red}{2.}$ 不成立)

proof:\
$\because , \text{indirectly connected} , \therefore , \beta \scriptstyle ij \normalsize = 0$

So what we want to prove now is $\boxed{c \scriptstyle ij \normalsize \leq 3 \alpha_j}$

Because the problem is metric,

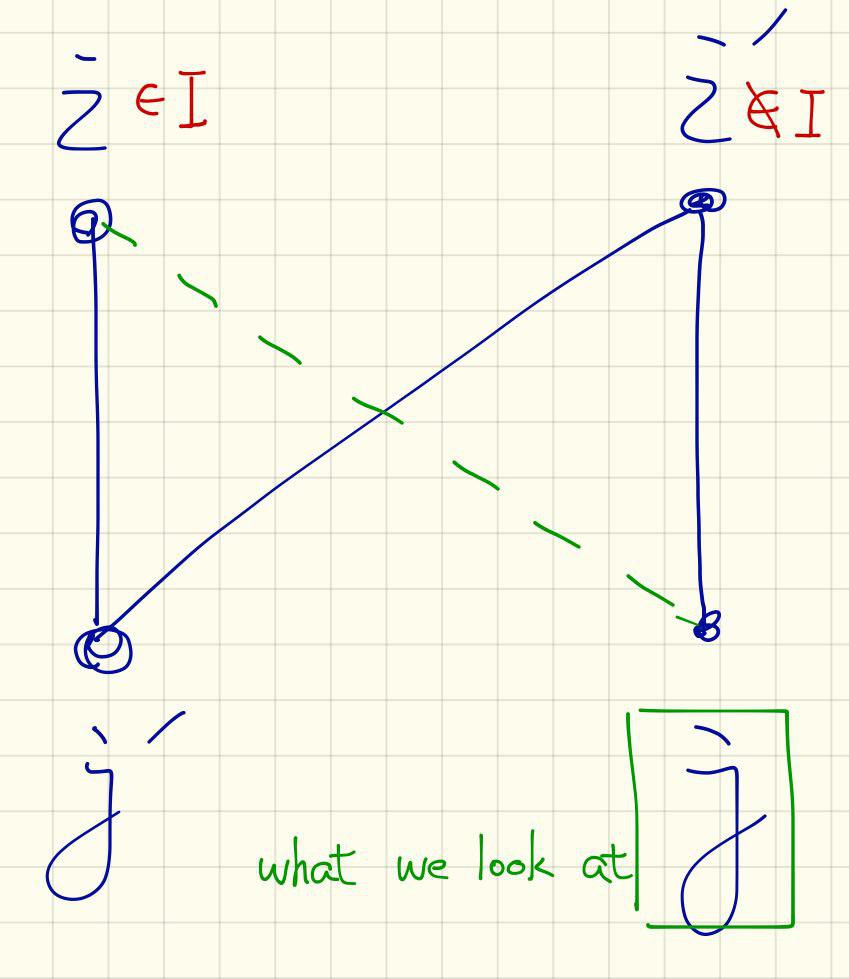
$$ \begin{align} c_{ij} & \leq c_{ij^\prime} + c_{i^\prime j ^\prime} + c_{i^\prime j}\\ & \leq \alpha_{j^\prime} + \alpha_{j^\prime} + \alpha_j \; (\because \, \text{for directly connected} \, \alpha = \beta + c \geq c\\ & \leq 3 \alpha_j \; (\because \alpha_j \geq \alpha_{j^{\prime}}) \end{align} $$

Note

如果 $i, i^\prime$ conflict， $(i,j)$ 又不 tight ，代表必定存在 $j^\prime$ 使得 $(i,j^\prime), , (i^\prime,j^\prime)$ 均為 tight 。\
如果說是 $i^\prime$ 比較早開，那麼 $\alpha_j, \alpha \scriptstyle j^\prime$ 會相等 (同時 fixed) ; \
但若是 $i$ 比較早開，$\alpha \scriptstyle j^\prime$ 比 $\alpha_j$ 提早被 fix ，一定比較小 $\Rightarrow \alpha_j \geq \alpha \scriptstyle j^\prime$

故我們可以將 $\color{red}{2}$ 式 relax 成以下

$$ \frac{1}{3} c_{ij} \leq \alpha_j - \beta_{ij} \leq c_{ij} $$

$\Rightarrow$ $\color{red}{\text{3-Approx. Algorithm}}$ ✌️

Reference

 
comments powered by Disqus