**Definition:**
A linear programming is a problem of maximizing or minimizing a linear
multivariate function subject to some linear constraints
Some Theorem
Thm. Feasible solution region is convex polytope
In N-simensional space, a polytope is called convex iff for any two points in the polytope, the line segment between these two points lies entirely in the polytope.
e.g $x_1, x_2$ is feasible, then $\lambda x_1 + (1-\lambda) x_2$ is also feasible ($ 0 \leq \lambda \leq 1$)
Thm. OPT happens at a extreme point
Thm. Linear Programming $\in$ P
e.g simplex method
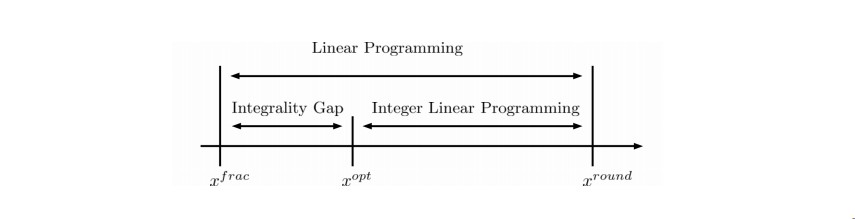
Integrality Gap
在解最佳化問題時,我們會將問題轉化成線性規劃的 form ,但某些 NPC 問題,要求演算法輸出的解需為整數,也就是 Integer Linear Programming Problem (Note that ILP $\in$ NPC)。我們會先將原先的 ILP 問題 relax 成 LP 問題,用現行的 LP solver 得到解後,根據這個結果去做 rounding,(either deterministic or randomized and more on this later),流程如下

在證明 approx ratio 時,關係如下
但近似的好度根據問題本身也有其上限,在此我們引進 Integrality Gap
Definition
The Integrality Gap (IG) is the upperbound of the ratio between $OPT$ and $OPT^{frac}$ over all problem instances. That is,
$\forall$ problem instance, 若我們能 follow LP relaxation and rounding 的步驟,\
得到一個 k-approx. algorithm ,使得 $\frac{\mathcal{C}(\text{round})}{\mathcal{C}(OPT^{frac})} \leq k$,便也可以推得 $\frac{\mathcal{C}(OPT)}{\mathcal{C}(OPT^{frac})} \leq k$
所以說 $k$ 便可以拿來當這個比例的上界,也就是 IG ,方能說明 Integrality Gap 為 $k$
Duality
對 minimizing problem 而言,考慮其 dual LP 問題,可以得到原先問題 (primal) 解的 lower bound (最好情況的 cost )。簡單來說,考慮以下的 LP 的標準型:
$$ \color{blue}{\min} 7x_1+x_2+5x_3 \enspace \text{subject to} \begin{cases} x_1 - x_2 + 3x_3 \geq 10\\ 5x_1 + 2x_2 - x_3 \geq 6\\ x_1,x_2,x_3 \geq 0 \end{cases} $$
要找 upper bound 很簡單,隨便找一組符合 constraint 的解代進 objective function 即可 。那麼若想找 lower bound 呢?我們不妨考慮將 constraint 做線性組合,去湊出 objective function 的係數,如以下
但這個下界鬆鬆的,若想讓它 tight 來找到 optimal 的 lower bound,我們需要設計 constraint 所乘上的係數 ($y_1, y_2$) 使得下界 tight ,而找到 optimal 係數的問題 (maximize $10y_1+6y_2$),可以表示成另一個 LP 問題,也就是所謂的 dual LP 。
Dual LP
$$ \color{green}{\max} 10y_1+6y_2 \enspace \text{subject to} \begin{cases} y_1+5y_2 \leq 7\\ -y_1+2y_2 \leq 1\\ 3y_1-y_2 \leq 5 \\ y_1, y_2 \geq 0 \enspace (\because \, \text{為滿足不等式相加依然滿足不等式的關係}) \end{cases} $$
General form
Primal LP
$$ \color{blue}{\min} \sum_{j=1}^{n}\color{orange}{c_j}\color{blue}{x_j} \enspace \text{subject to } \begin{cases} \sum_{j=1}^{n}a_{ij}\color{blue}{x_j} \color{blue}{\geq} \color{red}{b_i} \enspace \forall i = 1 \sim m \quad (m \, \text{個 constraints})\\ \color{blue}{x_j} \geq 0 \enspace \forall j \end{cases} $$
Dual LP
$$ \color{green}{\max} \sum_{i=1}^{m}\color{red}{b_i}\color{green}{y_i} \enspace \text{subject to } \begin{cases} \sum_{i=1}^{m}a_{ij}\color{green}{y_i} \color{green}{\leq} \color{orange}{c_j} \enspace \forall j = 1 \sim n \quad (n \, \text{個 primal obj. 的係數})\\ \color{green}{y_i} \geq 0 \enspace \forall i \end{cases} $$
Some theorem about duality
Thm. Weak Duality Theorem
$$ \text{If} \enspace \vec{x} \enspace \text{and} \enspace \vec{y} \enspace \text{are feasible}, \text{then} \sum_{j=1}^{n} c_jx_j \geq \sum_{i=1}^{m}b_iy_i $$
proof
$$ \sum_{j=1}^{n}\color{blue}{c_j}x_j \color{blue}{\geq} \sum_{j=1}^{n}\color{blue}{\sum_{i=1}^{m}(a_{ij}y_i)}x_j = \sum_{i=1}^{m}\color{green}{\sum_{j=1}^{n}(a_{ij}x_j)}y_i \color{green}{\geq} \sum_{i=1}^{m}\color{green}{b_i}y_i $$
Thm. Duality Theorem
$$ \text{If} \enspace \vec{x^\star}, \vec{y^\star} \enspace \text{are}\enspace OPT \enspace \text{for primal and dual}, \enspace \text{then} \enspace \sum_{j}c_jx_j^{\star} =\sum_{i}b_iy_i^{\star} $$
(Note that Duality Theorem DOESN'T hold for ILP)
Complementary Slackness
$$ \vec{x^\star}, \vec{y^\star} \enspace \text{are}\enspace OPT \enspace \text{for primal and dual}\\ \Updownarrow\\ \begin{cases} \forall j: \enspace \text{either} \enspace x_j^{\star} = 0 \enspace \text{or} \enspace \sum_{i=1}^{m}a_{ij}y_i^{\star} = c_j\\ \forall i: \enspace \text{either} \enspace y_i^{\star} = 0 \enspace \text{or} \enspace \sum_{j=1}^{n}a_{ij}x_j^{\star} = b_i \end{cases} $$
