Advanced Algorithm - Bin Packing Problem

Rounding Data & Asymptotic PTAS

Advanced Algorithm
Algorithm / Rounding Data & DP / Approximation Algorithm / NTU

從前兩講關於分配 (在一堆物品中，決定哪些是要拿的一群，哪些不拿) 的最佳化問題中，我們延伸出新的問題，Bin Packing Problem。不同於在 Knapsack Problem 中，我們只有一個箱子(可以想成你聘了一個工人搬一個箱子)；在Bin Packing 問題中，要取走所有寶物(所有寶物的重量都小於 1 單位)，而你需要聘請一些工人來搬，但今天每個工人都只帶了一個負重為 1 單位的箱子，該如何分配這些寶物(雖說是寶物，但其實我們不care價值惹)，使得需帶的箱子(聘請的工人)為最少？

簡單的 formulation 如下：

Given $n$ items with sizes $a_1 , a_2 , \cdots a_n$ , $a_i \in [0,1] \; \forall i$

Want: Find a packing in unit-sized bins to minimize # of bins
(WLOG, we can turn any problem instance to this formulation, omit those tedious rounding overflow issue :p )

2-Approx Algorithm

依序 iterate 過每個物品，將物品放到的一個可以放的下的箱子中(都放不下，就再開新的)。

PsuedoCode for First-Fit Algorithm

def first_fit(s_list):
  bin_ls = [0]
  for it in s_list:
    b_fit = False
    for bin in bin_ls:
      if bin + it.weight <= 1:
        bin += it.weight # put a_i into current bin
        b_fit = True
        break
    # no bins fit, open new one
    if not b_fit:
      bin_ls.append(it.weight)
  return len(bin_ls) # of bins used

Claim: If First-Fit Algorithm uses $m$ bins, at least $m - 1$ bins has $\sum \text{size} \geq \frac{1}{2}$

假設唯一那個負重小於 $\frac{1}{2}$ 的容器在第 $i$ 個位置，在它之前的 bins 一定都負重超過 $\frac{1}{2}$ (否則i-th bin 必可以整個放到前面的 bins)，而在它之後的 bins 也一定都超過 $\frac{1}{2}$ (否則就可以放到 i-th bin 了)。

$\text{OPT}$ $\geq$ $\sum_i a_i$ > $\frac{1}{2} (m-1)$
$\Rightarrow 2\text{OPT} > m - 1$
$\Rightarrow 2\text{OPT} \geq m$

NP-Hard

Bin Packing 是一個 NPC ， 但實際上在設計 Approximation Algorithm 時，也有一些先天的限制。

Thm. There is no $(\frac{3}{2} - \epsilon)$-Approx. Algorithm unless P=NP

Proof:
If total size is 2, OPT = 2 iff $\exists$ subset $S \, \sum_S\text{size} = 1$; otherwise, OPT $\geq$ 3
But if the poly-time algorithm can distinguish which case it is (i.e better ratio than $\frac{3}{2}$),
then we can use this algorithm to solve the 2-partition problem, which is NPC

$\Rightarrow$ There is no PTAS for Bin Packing Problem unless P=NP

Asymptotic PTAS

上例用一個 OPT 很小的例子來 claim 說 PTAS 不存在，但其實我們只不過才多用了一個箱子而已，但因為 OPT 小，所以多一兩個很嚴重。直覺來想，我們在 OPT 大一點時(差一兩個箱子沒差很多時)，可以得到更好的 approx ratio ，甚至能 derive 出 PTAS。對於這類問題，我們並不悲觀的認為找不到PTAS，但我們需要放鬆原先 PTAS 的限制，只在意那些 size 夠大的 instance， Asymptotic PTAS (APTAS) 應運而生。

Definition:

Given an $\epsilon > 0 \enspace \exists \, \text{algorithm} \, \mathcal{A} , n \in \mathbb{N} $   $\text{s.t} \, \mathcal{A} \, \text{is a } (1+\epsilon)\text{-approx. algorithm if OPT} \geq n$

($1 + 2\epsilon$)-Approx Algorithm

與之前的想法一樣，我們希望透由將原先的 problem instance 轉成方便我們求解的 formulation ，同時保有不太差的 performance guarantee 。這裡我們一樣要用到 rounding 的技巧，但在介紹如何 rounding 之前，我們先來想一下如何將問題變得比較簡單。
這裡的想法是直接窮舉所有的可能解，並從中挑出所需箱數最少者，但解的數目如果不做處理會是EXP，所以我們先丟掉某些 size 較小的物品( Intuitively, size 大者才會是 bottleneck 所在)，且同時減少不同的 item size (與之前 Knapsack, Subset Sum 在設計演算法時的想法相同)。

Lemma:
If there only $k$ different item sizes (且 size $\geq \,\epsilon$)， then exists poly-time algorithm can find the OPT

proof:

  1. number of ties in a bin $\leq M = \lfloor \frac{1}{\epsilon} \rfloor$ ( $\because \text{minimum size is} \, \epsilon$ )

  2. Only $\leq {H}^{k}_{M} = R$ different possible contents in each bin (那 $M$ 個位置選 $k$ 個物品)

  3. Total number of bin $\leq \, n$ (最多也才 $n$ 個物品)

$\Rightarrow$ Total possible output $ \leq \, H^{R}_n \, \leq \binom{n+R}{n} \, \leq \, n^R$ ($n$ 個箱子，每種都有 $R$ 種可能的物品重量組合可選)

雖然複雜度是 $\mathcal{O}(n^R)$( $R$ 還是一個很大的常數)，但至少我們把它壓在了 polynomial ✌

How to transform ?

所以現在我們該如何將任意的 problem instance $\textcolor{green}{\tilde{I}}$ ，轉成符合此 lemma 的 instance $J$ 呢？

首先我們將 size $ < \epsilon$ 者移掉得到 $I$，同時將剩下的物品依重量排序好，等個數地切分區間，每個區間有 $\lfloor n\epsilon^2 \rfloor$ 個物品 (最後一個區間可能會少，但不管)，將區間的物品重量都放大到下一區間的 minimum (最後一個直接設成 $1$)。

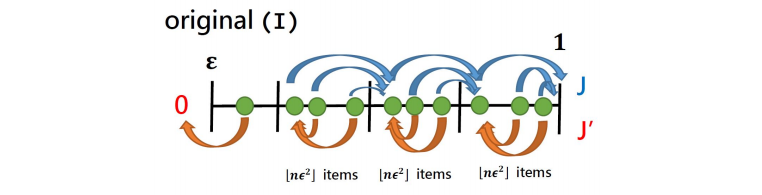
\[ \begin{cases} J: \text{將區間的元素放大到下一個區間的 minimum} \, \small \textcolor{red}{\text{(演算法所使用的)}}\\ J^{\prime}: \text{將區間的元素縮小到同一群的 minimum (第一個區間直接縮到0)} \, \small \textcolor{red}{(\text{用來證明bound})} \end{cases} \]

從這裡可以觀察到 $J$ 跟 $J^{\prime}$ 的差別只在 $J$ 多了 $\lfloor n\epsilon^2 \rfloor$ 個 size 為 $1$ 的元素。

$OPT(I) \, \geq \, \sum_{I}size \, \geq \, n\epsilon$
$\Rightarrow \epsilon \, OPT(I) \geq \lfloor n \epsilon^2 \rfloor$

$OPT(I) \leq OPT(J)$ ($\because J$ 是往上 rounding，所以在 $J$ 合法的解在 $I$ 中也會合法)
$= OPT(J^\prime) + \lfloor n \epsilon^2 \rfloor$
$\leq OPT(I) + \lfloor n \epsilon^2 \rfloor$ ($\because J^\prime$ 是往下 rounding)
$\leq (1+\epsilon) OPT(I)$ (根據上一個推導)

到這裡我們還不算成功，別忘了我們先移掉了那些比較小的物品(但我們直覺假設最後結果不太受影響)

接下來要把這些物品一個個加回去，使用我們前面的 2-Approx. algorithm: First-Fit

  1. First-Fit do not require any new bins $\Rightarrow OPT(J) \, \leq \, (1+\epsilon)\textcolor{green}{OPT(\tilde{I})}$

  2. First-Fit uses $\geq \, 1$ extra bins，
    假設最後用了 $L$ 個 bins ，那麼 all but the last bin must $\mathbf{\geq \, 1 - \epsilon}$ (否則可放至前面的 bins 中)
    $\Rightarrow \textcolor{green}{OPT(\tilde{I})} \, \geq \,\sum_{\textcolor{green}{\tilde{I}}}size > (L-1)(1-\epsilon)$
    $\Rightarrow \frac{\textcolor{green}{OPT(\tilde{I})}}{1 - \epsilon} > L - 1$
    $\Rightarrow L \leq \frac{\textcolor{green}{OPT(\tilde{I})}}{1-\epsilon} + 1 \leq (1+2\epsilon)\textcolor{green}{OPT(\tilde{I})} + 1 \, \square$

延伸問題

考慮另一個 NP-hard 問題，Minimum Makespan Scheduling Problem ，不同於 BP 的 constraint 在背包/箱子負重固定，希望 minimize 背包/箱子的數目；MSP 則是在可用的背包/箱子固定，但希望負重最大者負重不要太大。

Reference

 View    times
 
comments powered by Disqus