Subset Sum Problem 與 Knapsack Problem 相同,也是一個 NPC 問題(可以想成 Knapsack Problem weight 均為 1 的特例)。而在 Knapsack Problem 中,我們發展出等差 的rounding 技巧,犧牲精確度去換取更低的時間複雜度,而這一講中,將利用等比的方式去做 rounding 。
Algorithm
Computer $S_i$ : possible subset sum of {$v_1, v_2, \cdots ,v_i$}
$S_0 = ${$0$}
$S_1 = ${$\color{red}{S_0}, \color{blue}{S_0+v_1}$} = {$\color{red}{0}, \color{blue}{v_1}$}
$S_2 = ${$\color{red}{S_1}, \color{blue}{S_1+v_2}$} = {$\color{red}{0}, \color{red}{v_1}, \color{blue}{v_2}, \color{blue}{v_1+v_2}$}
.\
.\
.\
$S_{n} = $ $\color{red}{S\scriptstyle{n-1}}$ $\bigcup , (\color{blue}{S\scriptstyle{n-1}}$ $\color{blue}{+ , v\scriptstyle{n-1}}$ $)$
由 $S_{i}$ 計算 $S\scriptstyle{i+1}$ 以 $\mathsf{MergeSort}$ 來實做,並移除 $>W$的元素和 (複雜度為 $\mathcal{O}(|S_i|)$),又 $|S_i| < W , (\forall i=1 \sim n)$, 所以 Running time 為 $\mathcal{O}(nW)$。
可以發現複雜度與 $W$ 成正比,故充其量這個 Algorithm 也只是 psuedo-polynomial 而已,與前面的想法類似,造成複雜度的主因在每一個 Merge 的過程中,我們留下了太多元素(而 Merge 的複雜度又與元素個數呈線性),如果只取幾個代表性的元素(e.g $|S_i| = \mathcal{O}(\log W)$),便可將複雜度再往下壓。
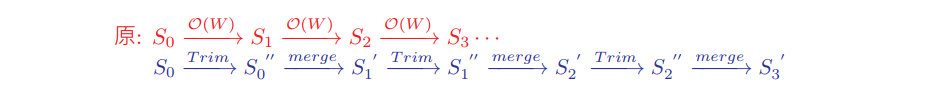
Pick $x_1$, remove elements $\leq \frac{x_1}{(1-\frac{\epsilon}{n})}$ in the list (say, $x_2 , \text{and} , x_3$). \
Then, pick $x_4$ and remove elements $\leq \frac{x_1}{(1-\frac{\epsilon}{n})}$ in the list. Repeat this procedure until the last element.
PsuedoCode for Trimming
def trim(s_list,delta):
ret = [] # trimmed list
last = 0
for elm in s_list:
if elm > last * delta:
ret.append(elm)
last = elm
return ret
Now, $|S_i| \leq \log_M W = \mathcal{O}(\frac{n\ln W}{\epsilon}) \Rightarrow \text{Total running time: } \mathcal{O}(\frac{n^2 \ln W}{\epsilon})$
Correctness Check

可以將 Trimming 視為改小某一 range 中的元素們(將其改至該 range 內最小的元素),OPT 在 trimming & merge 的過程中不斷地被改小,最多最多會被等比縮小 $n$ 次。
