Hashing 可以想成是一種 renaming 的方式,原先的名字 (key) 可能很長,但可能的組合並不完全隨機,且數量相對整個宇集少上不少,若我們要建立一個跟宇集一樣大的 Hash Table 並不符合成本(且大部份 slot 是空的),所以想透由 Hashing 的方式,重新命名 key’ ,並依據 key’ 將資料放到 size 跟資料個數差不多的 Hash Table 中。
定義
Given each data with key in $U = \lbrace 0,1, \cdots, t-1 \rbrace$,
A Hash Table is capable of performing the following operations in $\mathcal{O}(1)$
Insert(x)Delete(x)Search(x)
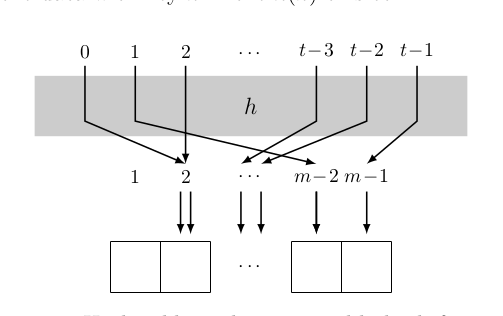
如同前面所述,$m \ll |U|$,所以hash function 必是 many-to-one mapping ,
也就是說,會有 collision 發生。而通常以下圖所示的 Chaining 來處理。
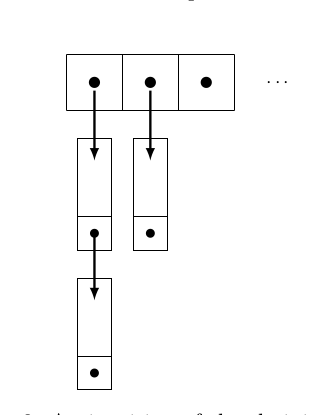
Hash Table 中所存的 element 為指向一個個 linked list 的 pointer。
在考慮 Chaining ,做複雜度的分析前,先假設我們有一 uniform hash function $h$,滿足以下性質
- $\Pr[h(k) = x] = \frac{1}{m}, x \in \lbrace 0,1,\cdots, m-1 \rbrace$
- $h(K_1),h(K_2),\cdots,h(K_n) \text{~are independent if} ~K_1,K_2,\cdots,K_n \text{~are independent}$
Average time complexity
[Theorem 1] Assume Uniform Hashing, $\mathbb{E}[op] = \mathcal{O}(\alpha)~~$ (Load Factor $~\alpha = \frac{ |\text{elements}|}{ |\text{slots}|} = \frac{n}{m}$)
可以觀察到,若 m = $\mathcal{O}(n)$,則 $\mathbb{E}[op] = \mathcal{O}(\alpha) = \mathcal{O}(1)$,
也就是說,只要 table size 跟元素個數是同個 order ,平均 來說,每個 operation 的 cost 還是 $\mathcal{O}(1)$。
Worst-case time complexity
現在我們想考慮在最差情況下的複雜度,
考慮一個類似的問題,將 $n$ 顆球 uniformly at random 地分到 $n$ 個 bin 中,
“the expected # of balls in the most loaded bin” 為何 ?
[Theorem 2] The max # of balls in any bin $\mathbf{\leq \frac{3\ln n}{\ln(\ln n)}}$ with probability $\mathbf{\geq 1 - \frac{1}{n}}$
$\underline{~Proof.} ~~~Let~k = \frac{3 \ln n}{\ln(\ln n)}~ \text{and}~ [S]^k \triangleq \lbrace A \subseteq S~ | ~|A| = k \rbrace$, $S$ is the set of balls
$$
\begin{aligned}
\Pr[\text{Bin} \; i \; \text{has}\, \geq k \; \text{balls}] & \leq \sum_{A \in [S]^k} \Pr[\text{Every ball in}~ A~ \text{is in Bin}~ i~] ~~(\because \textbf{Union Bound}) \\\\
& = \binom{n}{k} (\frac{1}{n})^k ~~(\because \textbf{uniform hashing}) \\\\
& = \frac{n!}{k!(n-k)!} ~ \frac{1}{n^k} = \frac{1}{k!} ~ \frac{n!}{(n-k)!n^k} \\
& \leq \frac{1}{k!} ~~(~\because~ \prod_{i=0}^{k-1}n-i \leq n^k) \\
& \leq (\frac{e}{k})^k \, (\because \, \text{Stirling formula as follows})\\
& \leq \color{red}{\frac{1}{n^2}} \, (\color{red}{\text{when} \; k = \frac{3 \ln n}{\ln(\ln n)}} \; \text{and according to the following lemma})
\end{aligned}
$$
[Theorem 3] Stirling’s approx. formula
[Lemma] $\forall \epsilon \in \mathbb{R}^{+} \; \exists \, n_0 \, s.t. \, \forall n > n_0 \, \boxed{\ln (\ln n) \leq \epsilon \ln n}$
Let $k = \textcolor{red}{\frac{3 \ln n}{\ln (\ln n)}}$
$$
\begin{align}
\therefore \ln (\frac{e}{k})^k &= k(1 - \ln k)\\
&= k[ \underset{\leq 0}{\underbrace{1 - \ln 3}} - \ln(\ln n) + \underset{\leq \frac{1}{3}\ln(\ln n)}{\underbrace{\ln(\ln(\ln n))}}] \\
&\leq k \cdot -\frac{2}{3} \ln(\ln n) = -2 \ln n \, \square\\
&\color{red}{\Rightarrow (\frac{e}{k})^k \leq \frac{1}{n^2}}
\end{align}
$$
Uniform Hashing?
看起來很合理,但當中我們做的一個假設其實是不合理的,也就是存在 uniform hashing function $h$ 這件事情,想完成這個條件只有以下兩種可能
- input is random (impossible !!)
- input is arbitary, but hash function is random
random hash function? 意思是說,我們希望有一組 hash function 的集合 $\mathcal{H}$,當每次要用到 hashing 時,便從中抽一個 $h: U \rightarrow \lbrace 0,1,\cdots,m-1 \rbrace$ 出來,可能結果很不好 ( collision 很嚴重, 可以想成總是可以構造出某些 input sequence ,讓特定的 $h$ 壞掉),在這種情況可以再重新抽,平均而言 collision 發生的機率很小即可 (i.e 不用太常重抽)。
我們希望 $\mathcal{H}$ 有以下性質:
$\forall x_1,x_2,\cdots,x_n \in S,~S \subset U,~ \text{and}~ a_1,a_2,\cdots,a_n \in \lbrace 0,1,\cdots,m-1 \rbrace$
- $\displaystyle \Pr_{h \in \mathcal{H}}[h(x_1) = a_1] = \frac{1}{m}$
- $\displaystyle \Pr_{h \in \mathcal{H}}[h(x_1) = a_1 ~\land~ h(x_2) = a_2 ] = \frac{1}{m^2}$ [Pairwise independence]
- $\displaystyle \Pr_{h \in \mathcal{H}}[h(x_1) = a_1 ~\land~ h(x_2) = a_2 ~\land~ \cdots ~\land~ h(x_n) = a_n ] = \frac{1}{m^k}$ [k-wise independence]
若想有 k-wise indep. 性質,則我們需要 $m^k$ 個 hash function $h$,需要 $\log |\mathcal{H}| = k \log m$ 個 bits 去記 $\mathcal{H}$ ,也就是說,若想要更好的隨機性, compute hashing 的成本就越高。
Let $L_x ~\text{be the length of linked list containing}~ x$
上例不需要用到 k-wise independence 這麼強的性質, pairwise independence 即符合我們的需要,也因此 2-Universal Hash Family 應運而生。
2-Universal Hash Family
$\mathcal{H}$ is 2-Universal iff for and two elements $x,y \in U ~\land~ x \neq y$
Example: Given $x=x_0 x_1 \cdots x_r~,y=y_0 y_1 \cdots y_r$, $a = < a_1,a_2,\cdots,a_r>,~a_i \in \lbrace 0,1,\cdots,m-1 \rbrace $
