這學期因緣際會之下,選了商研所的賽局,上起課來的感覺跟 EECS 著實差異頗大,直白的文字敘述及直覺居多(課後作業還是電影欣賞),考試也多以申論為主(但即使這樣,期中考還是考了全班最高分XD),碰巧在網路上找到了這門課程,覺得相當有趣,以資訊科學的角度出發, formulate 各種所謂「直覺」的經濟學想法,去解決現實世界的問題,聽了前兩堂課,感覺之後也會用到不少這學期修的高等演算法的概念,算是相輔相成,希望自己有毅力聽完,並整理筆記囉 :D
課程有以下三個部份
Mechanism Design
We want to design a system for strategic participants with good performance.
strategic 表示 agent/participant 會以自己的利益為第一優先 (i.e the objective is to maximize their own benefit),但是 good 與否則是由 designer 所定義的,而好的 mechanism 需要使 agent 與 designer 的 incentive 彼此間是互相 aligned 的,也就是說不好的 mechanism,會因 agent 追求自己的最大利益,而使結果不如 designer 預期。 (example: 2012 倫敦奧運的羽球女雙放水事件)
以下這段話相當有意思,也點明了 mechanism design 的重要性。
“ The burden lies on the system designer to anticipate strategic behavior, not on the participants to behave against their own interest. ”
像是說,如果沒有定義好股市的遊戲規則,那就不能怪罪有能力的商人去 exploit ,攫取自身的最大利益;又或是,若政府及企業沒有提供給人才適合的 pay 及發展環境,就不該冀望在人才外流時,他們還能能懷著愛國的情操留下來為國家奉獻一樣…
Can selfish behavior be near optimal
我們定義 Price of Anarchy (POA) 來描述自利行為與最優解 (everything is under control) 之間的比例 (一個 approx. ratio 的概念)
當 POA 越趨近於 1,表示自利行為越接近 optimal。
Example : Braess's paradox
考慮一群人要從 $ s \rightarrow t$,有兩種 type 的道路可選,其中一條 cost 為 constant 1,另一條的 cost 則是根據在其上的 agent 之比例 (如果全部的agent都通過此,則 cost = 1)決定。
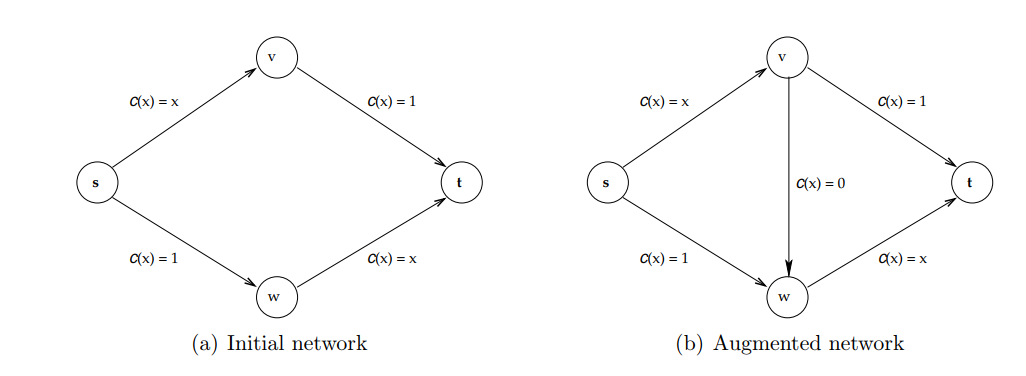
(The figure is from here)
未加中間的通道之前為 everything is under control (i.e 禁止 agent 走此 teleport ),其中 $c(x) = x$ 跟 $c(x) = 1$ 相比,至少都是前者較好,所以每個 agent 在可以選擇的時候,都會湧向 $c(x) = x$ 的道路。
(此例的 $POA = \frac{1 + 1}{1 + 0.5} = \frac{4}{3}$)
原因: Nash Eq. $\neq$ 社會最優
Corollary: Selfish routing DOESN'T minimize commute time
How do strategic players reach an equilbrium
在說明如何達到 eq. 之前,得先考慮該 eq. 是否存在
Nash Existence Theorem
If we allow mixed strategy, then every game with finite number of players who can choose finite number of actions has at least one Nash Eq.
確定了存在性,那 agent 該如何達到此 Eq. ?
課堂上概略提到了幾個 facts:
-
若是零和賽局,存在 $\mathbf{POLY}$ 時間的演算法求出 Nash Eq.
-
對非零和賽局而言,找 Nash Eq. 非 $\mathbf{NP-hard}$ 除非 $NP = coNP$
$\rightarrow \mathbf{PPAD-hard}$
我們利用 Nash Eq. 來作為預測 agent 行為的 predictor (同理,完全理性的 agent 在做出 action 時,也會考慮其他 agent based on 此而做出的的 action)。但第二個 fact 說明了一件事情,若我們承許 $P \neq NP$ ,則 Turing Machine 不存在有效率的解法找到均衡點,那算力不如它的 agent 更不可能找到均衡點,所以把 Nash Eq. 當作 agent behavior 的 predictor 就顯得沒有意義了… ☹
comments powered by Disqus