上一講提到了怎樣的 auction 是設計者所希望看到的,有足夠的誘因使參與者做出我們希望看到的決策 (DSIC property),且此決策所造成的結果為設計者認定的 optimal ,同時又能簡單到能在多項式時間完成。接下來會提供一個更 general 的方式去設計機制,而不單單只是限定於 single-item auction 而已。
Property of Awesome Auction
From Lecture2
- Incentive guarantee: DSIC property
- Computational efficiency: POLY time algorithm
- Performance guarantee: maximize the social surplus
在設計 mechanism 時,我們拆成以下步驟:
- 假設 bidder 會誠實報價,則我們該如何決定誰拿到 good (allocation rule) ,使得 (2), (3) 成立。
- 假設存在上述 rule ,那該如何定價 (payment rule) 使得 (1) 成立。
而這個 lecture 探討的為 step2,同時也透露了怎樣的 allocation rule 才會使對應的 payment rule 存在。
Single-Parameter Environments
首先我們將 single-item auction 推廣到更一般的 auction。
- n bidders, with valuation $v_i$ ($v_i$ 表示 bidder 的 max willingness for 1 unit stuff)
- feasible allocation $X = ( x_1,x_2,\cdots,x_n ) $ ($x_i$ 表示 i-th bidder 可以拿到幾單位的 stuff , 在 single-item auction 中,X 為一個只有一個 slot 為 1,其他全 0 的 vector)
Allocation and Payment Rules
Sealed-bid auction :
- 收集 bids $\vec{b} = (b_1, b_2, \cdots, b_n)$
- [allocation rule] Choose a feasible allocation $\vec{x}(b) \in X \subseteq \mathbb{R}^n$
- [payment rule] Choose payments $\vec{p}(\vec{b}) \in \mathbb{R}^n$
Quasilinear utility model
Definition
Implementable Allocation Rule
An allocation rule $\vec{x}$ for single-parameter environment is implementable
if $~\exists$ payment rule $\vec{p}$ such that the auction is DSIC
Monotone Allocation Rule
An allocation rule $\vec{x}$ for single-parameter environment is monotone
if for every bidder $i$ and other bids $b\scriptscriptstyle{-i}$, the allocation rule $x_i(z,b\scriptstyle{-i}$$)$ to $i$ is non-decreasing in its bid $z$
直觀意義上就是說喊價喊的越高,可以得到較多的 stuff,稍後的定理會證明以上兩個關於 allocation 的性質是等價的。
Myerson’s Lemma
Fix a single-parameter environment
- An allocation rule $\vec{x}$ is implementable iff it is monotone
- If $\vec{x}$ is monotone, then $\exists$ a unique payment tule such that the sealed-bid mechanism $(\vec{x},\vec{p})$ is DSIC (WLOG, assume $p_i(b_i) = 0$)
- The payment rule is given by explicit formula
Proof
利用 DSIC 的性質 (誠實為 dominant strategy),去列出不等式
Fix bidder $i$ and other bids $b\scriptstyle{-i}$,$0 \leq y < z$
case 1: ‘underbidding’ ($v_i$ 為 $z$ , 實際喊價 $y$)
case 2: ‘overbidding’ ($v_i$ 為 $y$ , 實際喊價 $z$)
在兩個 case 下都需要滿足,移項整理可得
利用夾擠定理,使得在某實數軸上每一點,$p(\cdotp)$ 都只有唯一的值
‘$\Rightarrow$’ : $\vec{x}$ is monotone $\Rightarrow$ x is implementable:
Fix $z$ and take the limit $y \rightarrow z$, 假設 $\vec{x}(\cdotp)$ is piecewise constant function
If there is no jump in $\vec{x}$ at $z$, $\Delta p = 0$
If there is a jump of magnitude $h$ at $z$, ($\Delta p$ at $z$) = ($z \cdotp$ jump in $x$ at $z$)
monotone 保證了 jump > 0,所以可以寫下 payment formula 為
其中 $z_1, z_2, \cdots, z_l$ 為 $x_i(\cdotp,$$b\scriptstyle{-i}$$)$ 在 $[0, b\scriptstyle{-i}$$]$ 的跳躍點
[Note] 可以將 payment formula 推廣到一般的 non-decreasing $\vec{x}(\cdotp)$
(2), (3)被證明
‘$\Leftarrow$‘: if $\vec{x}$ is NOT monotone $\Rightarrow$ x is NOT implementable (there is no way DSIC)
Just pick the points $a < b$, but $x(a) > x(b)$ as $y$ and $z$,
then the inequality of $\Delta p$ is broken
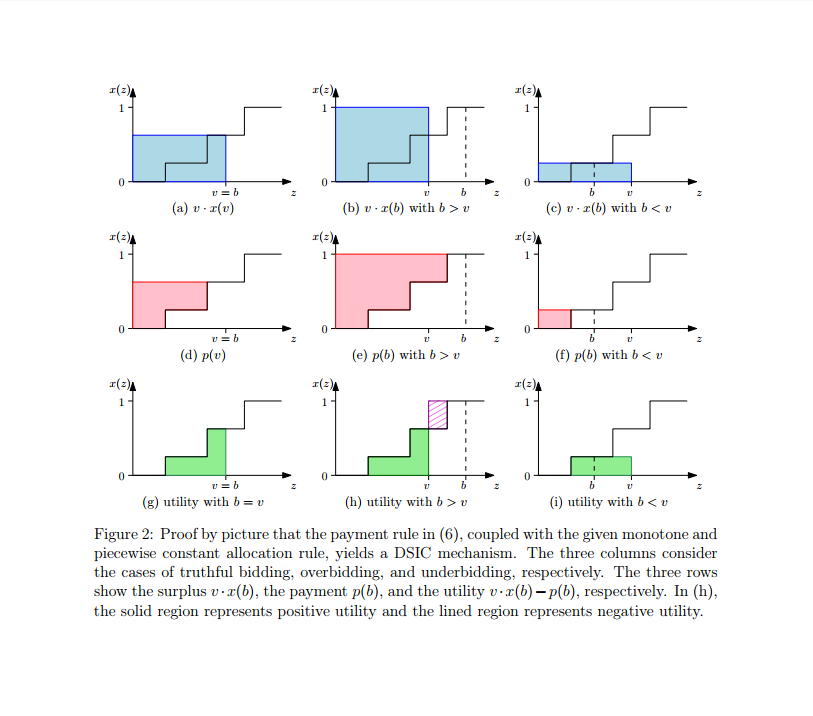
下圖以圖示證明 mechanism $(\vec{x},\vec{p})$ is DSIC (the figure is from the lecture)