Lec1 - Lec4 分別介紹了 Policy-based 及 Value-based 的 RL algorithm ,而這一講要 介紹的 Actor Critic 則是同時用到了兩個演算法的部份,並在 biased 與否 (準不準) 及 variance 高低 (好不好 train) 提供一個可以調控的 hyperparameter 讓我們選擇。
Motivation
目前為止介紹的 RL 演算法,想法都是在利用有限的 sample 去估測於 state $s$ 做出 $a$ 這個 action 相對於其他 action 的好度,也就是 $A^\pi(s,a)$ ( $Q^\pi(s,a)$ with normalization)。
Policy-based 的方法,並不 explicit 算出這個值,但在 update $\theta$ (which parametrize that policy) 時,利用了 final reward $r(\tau)$ (with some modification like baseline and causality to reduce variance) implicit 地當作 $Q(s,a)$ 的 sample,雖然是個 unbiased 的估計,但未來的變數太多, variance 太大的問題是 Policy Gradient 難 train 的原因。
而 Value-based 的方法,則是 explicitly 算出這個值,同時也提供了 biased 與 variance 的調控供選擇,而所對應的 policy 即是$\epsilon$-greedy 地選擇 action (with some modification to make it easier to train and more unbiased),但缺點在於很難 generalize 到 continuous action 的問題上。
而 Actor-Critic 則是想結合兩者,一樣利用 $\theta$ 去 parametrize policy,但利用 Value-based 的方法如 MC 或 TD 來近似 $Q^\pi(s,a)$
Advantage Actor-Critic
原先 Policy Gradient 的 $\nabla_\theta J(\theta)$
$$ J(\theta) = \sum_n \sum_t \nabla_\theta [\log \pi_\theta(a_t,s_t)] \color{red}{[\sum_{t^\prime = t}^{T_n} \gamma^{t^\prime - t} r_{t^\prime}^n - b ]} $$
紅色部份的第一項為 期望值為 $Q^\pi(s,a)$,我們不妨就直接拿 Q value 來代表,而 normalize 用的第二項很直覺地用 $V^\pi(s)$ 來代替
Remark: 在估 $Q,V$ 時,我們可以在 MD (#step $\rightarrow \inf$) 與 TD (#step=$1$)間,做 accurate 與 bias 的 tradeoff。
Fact
類似的概念,也可以用 Value Function 去 approx Q function。比如以下
以上是 1-step 的 case,很容易可以推廣到 multi-step (同樣是 bias 與 variance 的取捨)。
Remark: 也可以都用 $Q$ function 來表示 ( 對應的 $V$ 即是 Q value summation over action)
Remark: 實務上在 $V^\pi(s_{t+1})$ 會加上一個係數 $\gamma$ 作為 discount factor
綜合以上,以 1-step 的估計為例
$$ J(\theta) = \sum_n \sum_t \nabla_\theta [\log \pi_\theta(a_t|s_t)] \color{red}{[r(s_t,a_t) + \gamma V^\pi(s_{t+1}) - V^\pi(s_t))]} $$
Remark: $\gamma$ 也可以看成是一個 reduce variance 的技巧,畢竟越未來的事變數越多,variance 越大,所以當前決定中,越久之後才得到的 reward 不該影響這時候的決定太多。
Some tips
Shared Feature of policy and value approximator
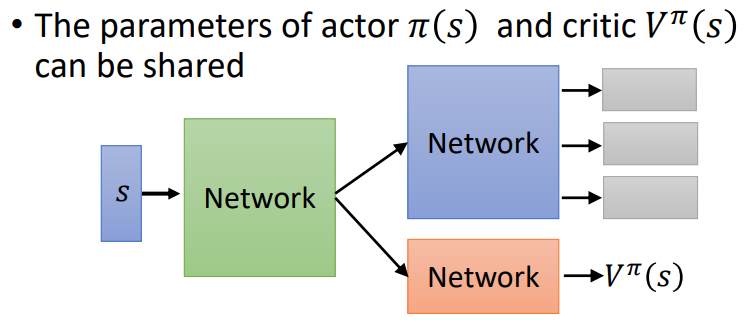
Async. Advantage Actor Critic (A3C)
平行化多個 agent 的學習,也是藉由增加 sample 量去減低 variance ,但參數的更新也會因 offline 的關係出現 bias。
