Reinforcement Learning - Lec4

Value-Based Algorithm - Training tips

Reinforcement Learning
RL / NTU / CS294

在這講中，要討論的是 non-tabular case 的問題 (就是上一講中無法保證收斂的那些QQ)，我們選定 Neural Network 作為拿來 approximate $Q(s,a)$ 的 function family，且不是用一般 regression 的方法找 $\phi$ (畢竟它的 target $y$ 也只是中間產物，並非 optimal Q)，而是 N-step 的 gradient descent。

Online Q-learning Alg. (N = 1)

  1. Take action to collect data
  2. $y_i = r(s_i,a_i) + \gamma \max_{a^\prime} Q_\phi (s_i^\prime,a_i^\prime)$
  3. $\phi \leftarrow \phi - \alpha \frac{dQ_\phi}{d\phi}(s_i,a_i)(Q_\phi(s_i,a_i) - y_i)$

Issue

  • $y_i$ relate to current param $\phi$ $\rightarrow$ non-stable

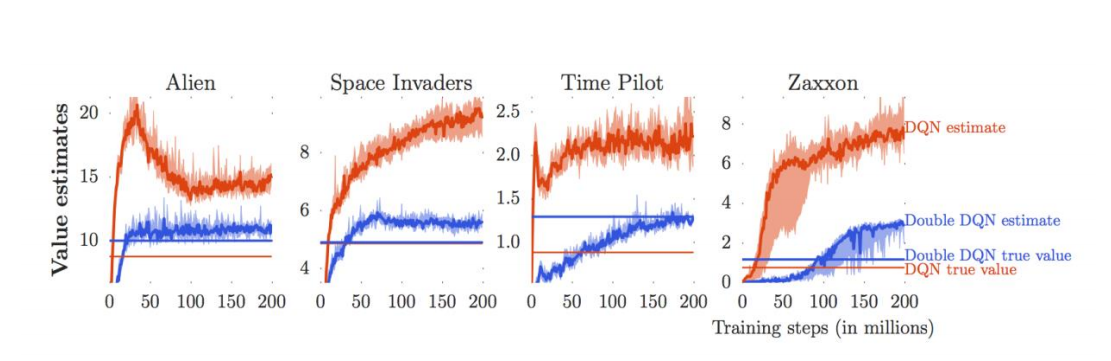
  • Q value 通常會 overestimate (因 max 的選擇，會 prefer overestimate 的 noise)

Double DQN (Target Network)

簡單來說，就是使用兩個 Q value NN，一個用來產生 target $y_i$ ，一個用來選擇 action ，實務上不會真的 train 兩個 network，而是用不同時間點的 network 參數 $\phi$, $\phi^\prime$ (等 $\phi$ 更新過幾輪之後，再 copy 給 $\phi^\prime$)

\[ y = r(s,a) + \gamma Q_{\textcolor{red}{\phi^\prime}}(s^\prime, \arg\max_{a^\prime} Q_\textcolor{blue}{\phi}(s^\prime,a^\prime)) \]

Some intuition

  • 在更新的過程中， target 會是 fixed 的，有助於 training 的穩定性
  • $Q_\phi$, $Q_{\phi^\prime}$ 引進的 noise 同樣都是 overestimate 的機率較原先小，更能準確的估 Q value

Prioritized Replay

一般來說，為了 batch training 需要，除了同時放多個 worker 下去更新$\phi$ 外，亦會將 sample 出的 training data collect 起來，存到 replay buffer 裡頭，每次 sample 一個batch 出來 update Q network

除了 uniformly sample from replay buffer 之外，也可以用以下 criteria 來決定sample 的 preference

  • large TD error 者 (需要加強訓練的 sample)
  • large Q value 者 (imply 好的經驗)

Multi-step

balance between TD (step = 1) and MC (step $\rightarrow \infty$)

Noisy Net

Instead of $\epsilon$-greedy when choosing action, add noise to $Q_\phi$ (will explore in consistent way)

Reference

 
comments powered by Disqus