上回提到了 policy gradint 的方法,及其缺點,這一講會介紹各種改進的方法。包括降低 sample 的 variance 及 off-policy (使得 data 更有效地被利用)。
Reduce Variance
Baseline
原先的 gradient 是以 $r(\tau)$ 作為 weight ,現在則是減去一個常數
$b \approx \mathbb{E}[r(\tau)]$。
想法是可能每個 $\tau$所收到的 reward 都是正的,在下一次更新後,
policy 更會 prefer 去選擇這些 $(s,a)$ ,但因為畢竟我們是用 sample 的方式,尚有許多 $(s,a)$ 沒有遇到,reward 相當於是 $0$ ,但其可能是個比平均好的選擇,在原先的 policy update 卻不會被 explore 。\
簡單來說就是要 normlize reward。
Remark: 減去這個項所得的新 weight ,相較原先的 final reward 是 unbiased sample。
Causality
Action taken at $t^{\prime} (> t)$ cannot affect reward at $t$
將原先的 $r(\tau)$ 取代成 $\sum_{t=t^{\prime}}^T \gamma^{t - t^{\prime}}r_t$
Note: $\gamma$ 為 discount factor (of time)
Remark: 把 gradient 的 weight 稱為 Advantage function $A^\pi(s_t,a_t)$\
意義上為 “How good it is if we take $a_t$ than other action at
$s_t$” 。
Off-policy
原先 naive 的 REINFORCE ,在學/要更新的 agent (parametrized by $\theta$) 跟與環境互動的 agent/actor 是同一個,我們稱此為 on-policy,但這樣的壞處在於 trajectory collection 耗時,而且一旦參數更新了,又要再次 resample ,非常沒有效率。
故引進 off-policy 的方法,重複使用之前獲得的 trajectory,但這樣的 tradeoff 在於所計算的 gradient 可能不精確 (不適合現在的 agent),所以需要的 constraint 去減緩這件事情的影響。
Importance Sampling
假設現在我們有兩組 trajectory distribution $p,q$,我們想利用從 $q$ 所 sample/collect 的 trajectory 去更新 $p$ (will update coresponding polcy),那麼該如何估測 Policy Gradient 所需要的 expected reward $\mathbb{E}_{\tau \sim p}[r(\tau)]$? 這時候就需要用到 Importance sampling,推導如以下
$$ \begin{aligned} \mathbb{E}_{\tau \sim p}[r(\tau)] &= \int_\tau p(\tau) r(\tau) d \tau\\ &= \int_\tau r(\tau) \frac{p(\tau)}{q(\tau)} q(\tau) d\tau \\ &= \mathbb{E}_{\tau \sim q}[r(\tau) \color{blue}{\frac{p(\tau)}{q(\tau)}}] \end{aligned} $$
Remark: $\frac{p(\tau)}{q(\tau)}$ 稱為 importance weight ,用此 去 scale 相對應的 reward。
Remark: 儘管期望值相同,但 $\text{Var}\scriptstyle{\tau \sim p}\textstyle[r(\tau)]$ 和 $\text{Var}\scriptstyle{\tau \sim q} \textstyle[r(\tau) \frac{p(\tau)}{q(\tau)}]$還是不同的。兩個 distribution 還是不能差太多,這也是 要加 constraint 的所在。
下面有一張簡單的示意圖(不過 notation 有點小不同😅)
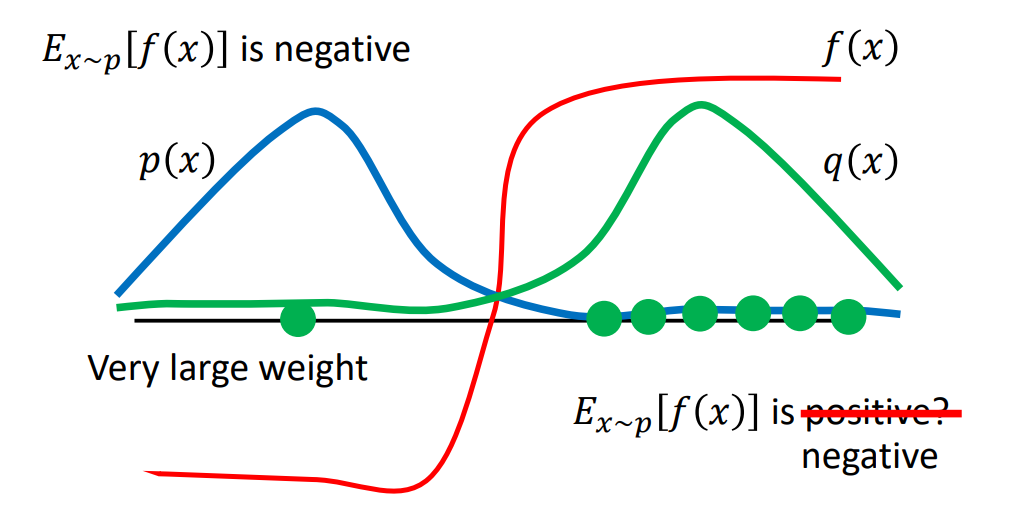
Proximal Policy Optimization (PPO)
將原先的 objective function $J^{\theta^\prime}(\theta)$ 加上一個衡量 $\theta,\theta^\prime$ 對應 policy 的 KL divergence\
(拿上面的例子來看的話,就是 $\text{KL}(p,q)$)
Remark: 另外有一個變形,不是考慮 policy 的 KL divergence,而是用一個 function 去 clip $\frac{p(\tau)}{q(\tau)}$ 差太多的情況。
Remark: 不過實務上 update 幾次後,不可避免地還是要重新 sample。
