前一講提到了無論是 stochastic noise 或是 ground truth 過複雜而引進的 deterministic noise ,對本身就複雜 (VC dimension 高) 的 model 而言,overfitting 是很容易發生的,而解決之道其一就是這一講所要介紹的 Regularization。
除了藉由 cleaning 或 augumentation 等改變原始 data distribution $\mathcal{D}$ 的方法之外, regularization 派的方法主要藉由降低 hypothesis set 的複雜度來減少 $\Omega$ 的 penalty term 以縮小 $E_o$ 及 $E_i$ 的差距。如以下:
Regularization 有很多種實現的方式,而這裡會介紹最常見的一種 - Weight Decay ,藉 由 prefer 在 $\mathbf{0}$ 附近的 $h$ (i.e $||h||$ is small)來減少 overfitting 。
General Idea
到這裡可能多數人會有一個疑問,為什麼選擇 norm 小的 model 就會是好的選擇呢?
Heuristically 來說, Regularization 想解決的是 noise 的影響(non-smooth and high-freq),而我們想 model 的那 些 ground truth empirically 來說參數都不太大 (strong hypothesis … lol),所對應的 surface 也是較為平滑的,這也是為什麼 weight decay 會有用的原因。
相信這大概沒有回答到問題,不如來算點數學吧☺
Step back to simple (low-order) model
回顧前一講的兩個實驗,low-order 的 hypothesis $\mathcal{H}_2$受到 overfitting 的影響較 high-order 的 $\mathcal{H}\scriptstyle 10$來說較不嚴重,所以不妨限制 $\mathcal{H} \scriptstyle 10$ 的某些係數為 $0$ 來降 order 。
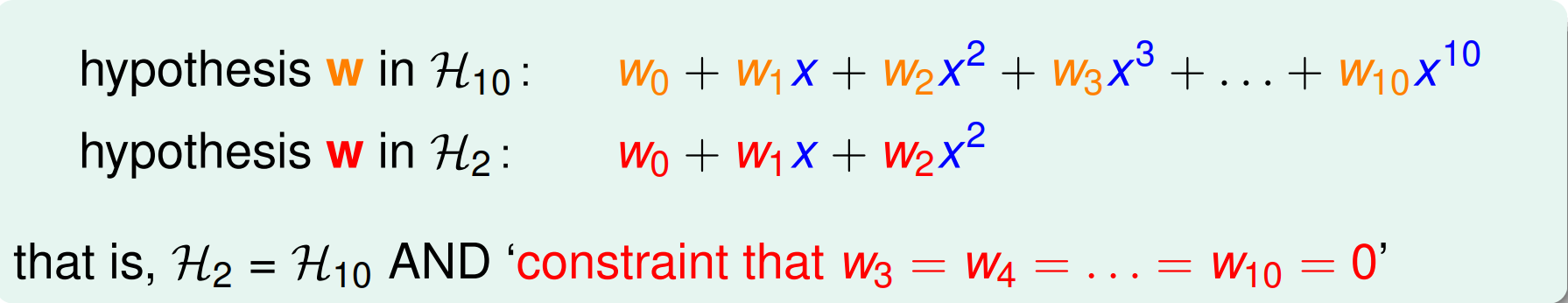
不過這樣還蠻愚蠢的,那打從一開始用 $\mathcal{H}_2$ 就好了😅
Looser but Hard Constraint
所以我們稍稍放寬限制,限定只要係數不為 $0$ 的 $w_n$ 不要太多就好,如以下
這樣的好處是我們比原先 low order 的 $\mathcal{H}_2$ 更具彈性,但同 時又比 $\mathcal{H} \scriptstyle 10$ 還安全,然而, boolean 的 constraint 是很難 optimize 的 (which is NP-hard),所以我們不妨將其轉成較好 optimize 的形式 (但同時又 align 我們原先的 motivation)
Soft Constraint
Given $C \geq 0$, we have regularized $\mathcal{H}( C )$ with the following constraint
Remark: 當 $C$ 足夠大的時候,其實對解完全不影響 (i.e 就 linear regression 這種可以找 closed-form 的問題來說,只要 $\sqrt{C}$ 的 高維球有把原先的 optimal sol $\mathbf{w}_{lin}$ 包進去, regularized term 就不會發揮作用)
Geometric View
那麼在 regularization 下,找到的 $\mathbf{w}_{reg}$ 有什麼特性呢 ?從幾何上來看
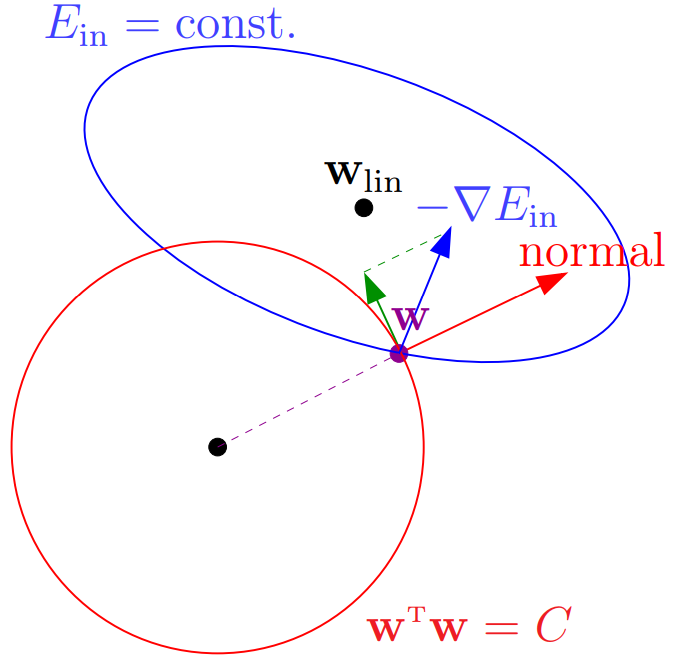
所有的合法解會在 $\mathbf{w}^T \mathbf{w} = C$ 上的球移動,而停止的 criteria 是 $\nabla E_{in}$ 已經再沒有在球上移動的切分量,亦即
而我們想找到一個 $\lambda > 0$ and $\mathbf{w}_{reg}$ 滿足
Remark: $\lambda$ 稱為 Lagrange Multiplier ,是一個在
constraint 下 解 optimization 問題的 方法 trick。
Equivalent Augumented Error
要解上方那個 Equation 等價於 minimize 以下這個 objective
Remark: 對不同的 $C$ ,均有對應的 $\lambda$ ,而 $E_{aug}$ 將 $\sqrt{C}$-hypersphere 這個 constraint 轉成藉由調控 $\lambda$ 大小的 unconstrained optimization 問題,實務上也比較好做。
Remark: 技術上來說,在 unconstrained optimization 中,我們還是享有整個 $\mathcal{H}$ 的 flexibility 。
