我覺得自己之前做的投影片真的蠻好的XD (自己講),因此這一講中,只會偏重在原本寫的比較簡略的 Learning Problem , Evaluation 及 Decoding Problem 僅會附上程式碼及做定義。
3 Problems of HMM
Given observation sequence $X$ and model parameter $\Theta$
$\Theta$ 包含了以下幾個 component: $\pi$ (initial probability), $A$ (transition matrix), $\phi$ (emission probability)
-
Evaluation Problem: $\Pr(X|\Theta)$,即是一開始我們想求的,該 sequence 與特定 HMM match 的 likelihood,可用於 isolated word recognition 。
-
Decoding Problem: Find the optimal state sequence $\Pr(Z|X,\Theta)$ (在之後的 continuous ASR ,我們需要知道一路走來的 state sequence,才能據此還原出對應的 word sequence)
-
Learning Problem: Find the optimal parameter $\Theta^\star$, which satisfies some criteria
Evaluation Problem
Solution: Forward Algorithm
$$ \alpha_t(i) \triangleq \Pr(x_1,x_2,\cdots,x_t \land z_t = s_i | \Theta) $$
因為在最後一個 frame 中, $\alpha_T(i)$ 跟 $\alpha_T(j) , (i \not = j)$ 中的事件互斥,所以我們可以對 $\Pr(X|\Theta)$ marginalize over states
$$ \Pr(X|\Theta) = \sum_{i=1}^M \alpha_T(i) $$
logalpha = np.zeros((num_frame,num_state))
for j in range(num_state):
logalpha[0][j] = log_startprob[j] + log_emlik[0][j]
for i in range(1,num_frame):
for j in range(num_state):
logalpha[i][j] = logsumexp(logalpha[i-1,:]+log_transmat[:,j]) +log_emlik[i][j]
return logalpha
Decoding Problem
Solution: Viterbi Algorithm
$$ \delta_t(i) \triangleq \max_{Z_{-t}} \Pr(Z_{-t},X \land z_t = s_i | \Theta) $$
logdelta = np.zeros((num_frame,num_state))
ptr = np.zeros((num_frame,num_state),dtype=np.int8) # the first row is dummy
best_path = np.zeros(num_frame,dtype=np.int8)
for j in range(num_state):
logdelta[0][j] = log_startprob[j] + log_emlik[0][j]
for i in range(1,num_frame):
for j in range(num_state):
tmp = logdelta[i-1,:] + log_transmat[:,j]
logdelta[i][j] = np.max(tmp) + log_emlik[i][j]
ptr[i][j] = np.argmax(tmp)
best_path[-1] = np.argmax(logdelta[-1,:])
for i in range(2,num_frame+1):
best_path[-i] = ptr[-i+1][best_path[-i+1]]
return np.max(logdelta[-1,:]), best_path
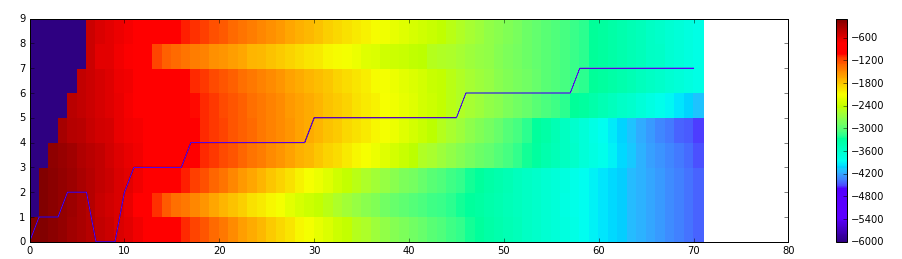
Remark: 亦可利用 Viterbi 算出來的機率,去近似 forward algorithm 所計算的結果 (從下圖 Viterbi 的best path 之走勢與 logalpha 的變化可略知一二)
Learning Problem
Solution: Baum-Welch Algorithm (a special case of EM algorithm)
一個 HMM model $\Theta = \lbrace \pi, A, \phi \rbrace$ 我們想根據 data 去調整 $\Theta$ ,使得其能 exploit 去選出較好的參數 $\Theta^\prime$,而所謂的好,可能是
- fit data (e.g likelihood, posterior) -> ML, MAP criteria
- classification performance (discriminitive training)
在此我們考慮 ML (Maximum Likelihood) criteria ,也就是想找到 $\Theta^\star = \underset{\Theta}{\arg \max} \Pr(X|\Theta)$
對 HMM 來說,直接從 $\Theta$ 是不能直接去估 $X$ 的分佈的,必須要先確定所對應的 state sequence $Z$ 才行,但今天難點就在 state 是 hidden 的。\
EM Algorithm (Expectation-Maximization) 常用來解決這類問題,大概的思想就是:
- E-step: 利用現在的 parameter $\Theta$ 去算背後 state 分佈的期望值 (白話來說就是假設知道了 state)
- M-step: 知道了 state 的分佈,去估計 HMM 的參數 (to maximize some criteria)。
E, M iteratively 交錯去更新參數。
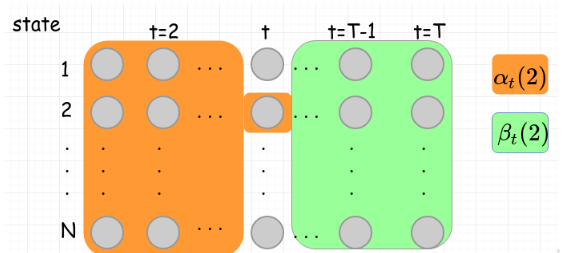
E-step
先定義一些值
Backward Probability
跟 forward probability $\alpha_t(i)$ 很類似,不過是考慮後半
$$ \beta_t(i) \triangleq \Pr(x_{t+1},x_{t+2},\cdots,x_{T}|z_t = s_i, \Theta) $$
logbeta = np.zeros((num_frame,num_state))
for j in range(num_state-1,-1,-1):
logbeta[num_frame-1][j] = 0
for i in range(num_frame-2,-1,-1):
for j in range(num_state):
logbeta[i][j] = logsumexp(logbeta[i+1,:]+log_emlik[i+1,:]+log_transmat[j,:])
return logbeta
Posterior Probability
Gamma Probability
$$ \gamma_t(i) \triangleq \Pr(z_t = s_i | X,\Theta) = \frac{\Pr(z_t = s_i ,X | \Theta)}{\Pr(X|\Theta)} = \frac{\alpha_t(i) \beta_t(i)}{\underbrace{\sum_j \alpha_T(j)}_{\text{Evaluation Problem 算過}}} $$
Remark: $\sum_{t=1}^{T-1} \gamma_t(i)$: $\mathbb{E}[X$中有拜訪過 $s_i$$]$,同時也是在 $s_i$ 中**有發生 transition** 的期望值。
Epsilon Probability
$$ \epsilon_t(i,j) \triangleq \Pr(z_t = i \land z_{t+1} = j | X,\Theta) $$
$$ \epsilon_t(i,j) = \frac{\alpha_t(i) A_{ij} \phi_j(x_{t+1}) \beta_{t+1}(j)}{\Pr(X|\Theta)} $$
Remark: $\sum_{t=1}^{T-1} \epsilon_t(i,j)$: $\mathbb{E}[s_i \rightarrow s_j]$
Note: 上述這兩個機率都是 conditioned on 整個 observation sequence $X$ ,而非只有那個時間點的 $x_t$
M-step
Initial Probability
$$ \pi_i = \gamma_1(i) $$
Transition Probability
$$ A_{ij} = \frac{\mathbb{E}[s_i \rightarrow s_j]}{\mathbb{E}[\text{# of visit}\, s_i]} $$
Emission Probability
前面提到,我們利用 GMM 來 model emission probability (mixture 數夠多可以近似任何的連續函數,我想也是有 optimization feasibility 的考量)
在選定該時間點對應到哪個 state 後,還要在從一把 gaussian 中抽出一個去 sample observation $x_t$。(pretty hierachical XD)\
$$ \phi_j(x) = \sum_i w_{jk} \mathcal{N}(x;\mu_k,\sigma_k^2) \quad(w_{jk} \, \text{為 k-th Gaussian 在 state j 的 GMM 中所佔的比例}) $$
要重估的參數有每個 gaussian 的 mean 和 covariance 以及 在某個 mixture 的比例 $w_{jk}$
Note: 上面的 $x_t, \mu, \sigma^2$ 都可以是向量形式
Remark: 我們假設 $d \times d$ 的 covariance matrix 是 diagonal (based on 前面抽 feature 時,用 DCT uncoorelate feature 的各個 dimension)
Posterior Probability of choosing k-th mixture
$$ \begin{aligned} \gamma_t(j,k) &= \Pr(z_t = s_j \land \text{choose k-th mixture in state j} |z_t = s_j, X, \Theta)\\ &= \underbrace{\quad \gamma_t(j) \quad}_{\text{gamma probability}} \cdot \underbrace{\frac{w_{jk}\mathcal{N}(x_t;\mu_{jk},\sigma_{jk}^2)}{\sum_m w_{jm}\mathcal{N}(x_t;\mu_{jm},\sigma_{jm}^2)}}_{\text{k-th mixture 佔的比例}} \end{aligned} $$
Update Rule
$$ \begin{aligned} w_{jk} &= \frac{\mathbb{E}[\text{# of choosing k-th mixture in state j}]}{\mathbb{E}[\text{# of visit}\, s_j]} = \frac{\sum_t \gamma_t(j,k)}{\sum_t \gamma_t(j)}\\ \mu_{jk} &= \frac{\sum_t \gamma_t(j,k) x_t}{\sum_t \gamma_t(j,k)}\\ \sigma_{jk}^2 &= \frac{\sum_t \gamma_t(j,k)(x_t - \mu_{jk})^T (x_t - \mu_{jk})}{\sum_t \gamma_t(j,k)} \end{aligned} $$
Remark: 跟一般沒有跟 HMM bind 在一起的 Gaussian Mixture 更新基本上一樣,但
- sample 數 $N$ 改為 $\mathbb{E}[\text{number of visit}, s_j]$ (因為這個 mixture 不是每次都會被抽到,要拜訪 $s_j$ 才是它負責的);
- $\gamma(j,k)$ 多了一個下標 $t$ (時間 $t$ 在 state $j$ 且抽中該 Gaussian 的期望值),表示其會隨 time evolve
Remark: 而 GMM 的更新,就是根據想 maximize 的 criteria 定義 loss function ,去微分求極值發生點。
comments powered by Disqus