在能夠將聲音訊號轉為數值向量給 machine 處理後,我們要怎麼判斷這串 vector 是 mapping 到哪一段文字呢? \
在進入 continuous ASR 前,讓我們先來想一想怎麼辨識一個 word ?想法是針對這個 word 建一個 model ,給定一段聲音訊號, output 該訊號 map 到此
word 的機率為多少。
Characteristic of Speech
聲音訊號的特性在於,每個時間點的數值,會與 context 相關,也就是說
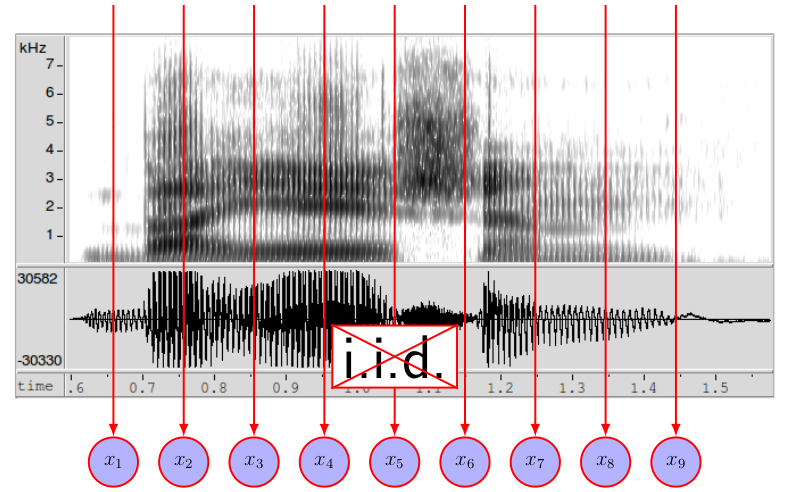
所以我們的 model 除了要包含每個時間點的 distribution ,也要考慮之間的 transition。
Probabilistic Model
同時考慮的話,就是對每個時間點的訊號 $x_t$ ,我們要去計算其 given 之前時間點的訊號($\mathbf{x} \scriptsize -t$) 的條件機率 $\Pr(x_t|\mathbf{x}\scriptsize -t)$, 可以利用 Bayesian Network 去描述。
但今天隨著訊號長度變長(frame 數變多),我們需要去估計的機率也越來越多,\
考慮 $\mathbf{x} = \lbrace x_1,x_2,x_3 \rbrace$,想計算 $\Pr(\mathbf{x})$,要有 $\Pr(x_1) \times \Pr(x_2|x_1) \times \Pr(x_3|x_1,x_2)$ ,當中的每一項都是需要估計的。但這樣複雜度實在太高,故我們引進以下的假設:
- First order Markov Assumption ($x_t$ 只與其前一個聲音訊號有關)\
$\Pr(x_t|\mathbf{x} \scriptsize -t \normalsize) = \Pr(x_t|x_{t-1})$ - 假定每個 frame sample 都是從一個 distribution 抽取出來,而這個 distribution 會
隨著時間變化,但不同的 distribution 數目是有限的。\
引進 latent variable $z_t$ (或者說 state variable),每個不同的 state 對應到不同的 distribution (但不同時間點,若 state 相同的話,則 distribution 是一樣的, i.e stationary)
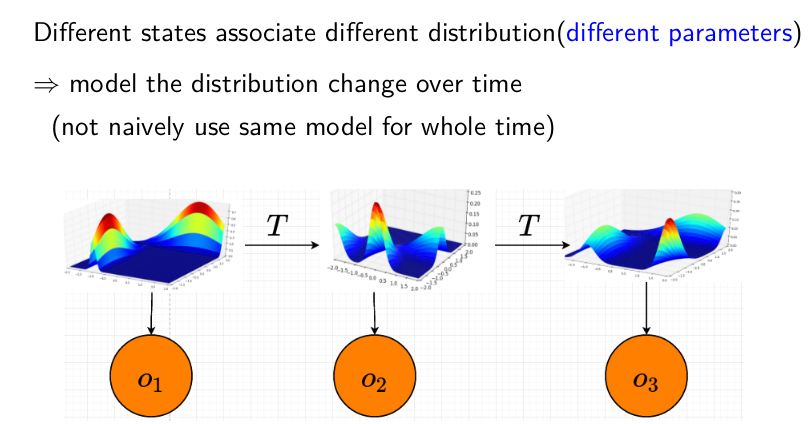
- $x_t$ (也是上圖的 $o_t$) 只跟 $z_t$有關,而 $z_t$ 根據 Markov assumption 只跟 $z_{t-1}$ 有關。
Hidden Markov Model
HMM 就是做了以上假設的產物,也是我們拿來 predict 聲音訊號跟該 word 所對應的 HMM match 機率的 model。 我們需要計算以下機率值
- Emission Probability: $\Pr(x_t|z_t) , \forall t$
- Transition Probability: $\Pr(z_t|z_{t-1}) , \forall t$
- Initial Probability: $\Pr(z_1)$
Remark: HMM 所 model 的,可以想成是 ASR 的基本 unit ,選 word 是一種選擇,但在 continuous speech 中,我們通常會選用更短的單位 - phoneme (並以 3 個 state 去描述),然後再利用 lexicon model (這個 word 是怎麼發音的 i.e 怎麼被 phoneme 組成的) 將其串成一個大 HMM 以辨識 words (算是對那些不同 word 中,發音相同的部份做 weight sharing,這個概念之後也會很常用到)。
延伸閱讀
在此提供一份之前報告所作的投影片
comments powered by Disqus