上一回介紹了 LPC ,來做為我們抽取 feature 的一個方法,今天要來談談目前最常被使用的 feature - MFCC 。
Background
LPC 所求得的係數用來 model 發聲時唇齒舌的構造所對應的 filter ,但這個 model 的假設是該 filter 為 all-pole (但我不知道為何不也 model zero ^^”),所以對某些音來說效果會沒這麼好 (e.g nasal (鼻音))。而今天所介紹的 MFCC 摒除了這個假設,並將人類聽覺的一些學理基礎 (filter bank) combine 進 model 當中。
Remark: 很簡單很簡單地來說, LPC 像是藉由觀察一個人的唇齒舌之位置,去猜測他說了什麼,而 MFCC 除了這點之外,還多模擬人類聽聲音的過程 (查閱文獻後,其似乎也只應用在 speech recognition 的 scenerio)。
流程
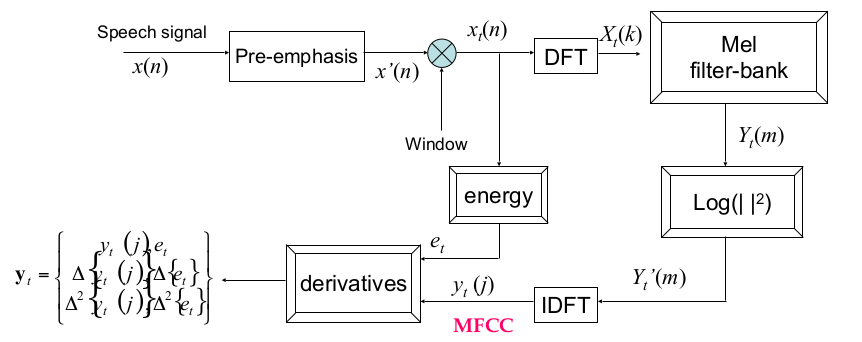
以下會針對每個 component 做說明,另外,我把 step-by-step 跑出 MFCC feature 的 ipynb 放在這裡(語音資料來自 KTH DT2119 所提供的 TIDIGIT)
Pre-emphasis
在發聲的時候,高頻部份的聲音通常較弱 (尤其是 voiced speech),因此為了 catch 到在高頻的 formant ,我們會讓訊號經過一個 High-Pass filter (下圖紅色線是有 pre-emphasis 過的)
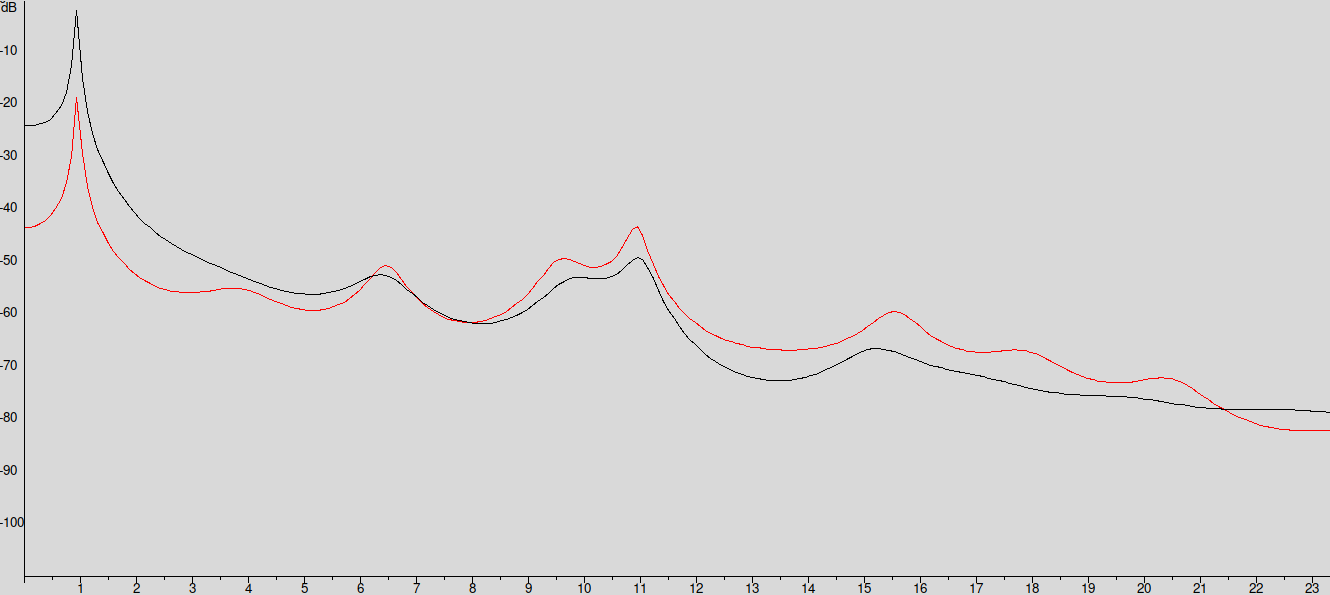
那這個 filter 怎麼描述呢?
$$ y[n] = x[n] - \alpha x[n-1] $$
$$ H(z) = \frac{Y(z)}{X(z)} = 1-\alpha z^{-1} $$
signal.lfilter([1,-ALPHA],[1],input,axis=1)
Impulse Response 如以下
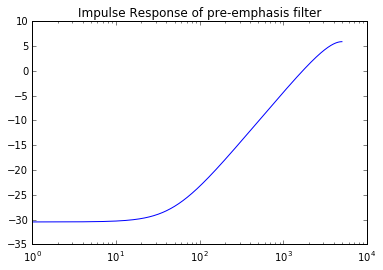
你也可以在 ipynb 中聽聽看 pre-emphasis 前後聲音訊號的差別 (後者聽起來比較清晰)。
Hamming Windowing
在下一步中,我們要將 time-domain 的訊號經由 Fourier Transform 轉成 spectrum ,但今天訊號長度有限( 因為 sampling rate 有限的緣故),轉出來的頻率值數目也要有限,所以是使用 DFT 。但做 DFT 時,數學上來說,我們是針對 infinite periodic time signal (將原先的 signal 往兩側 copy-paste 無限次)做 Fourier Transform,所以如果今天頭尾不連續的話,相當於是引進了不連續點 (impulse) ,會讓頻譜多了無關的雜訊,因此常常 apply Hamming Window (如以下),去讓頭尾都能接到 $0$。
ham_window = signal.hamming(WINDOW_LENGTH,sym=False)
windowed = ham_window * input # elementwise mul.
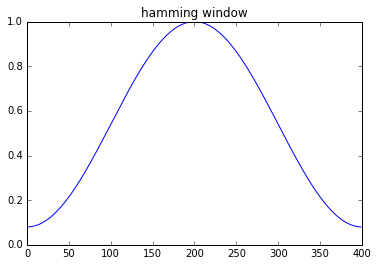
Remark: 但也不是說 Rectangular window 就一定不能用啦…
DFT & Mel-scale Filter Bank
這部份就是整個 MFCC 最精華的地方了,DFT 之後,對每個 frame 我們都有其相對應的頻譜 (一把 freq. 值),正常人耳聽到聲音時,會有不同的受器去感知不同的頻率,經由電訊號傳導進而在腦中形成聲音。
我們可以把這些受器 model 成 bandpass filter (這裡是利用 triangular filter)。另外,它是 distribute logarithmically 於頻率軸上。 (也就是說,在低頻部份,所擁有的濾波器數量是比較多的,人類比較能夠辨別不同頻率的低音)

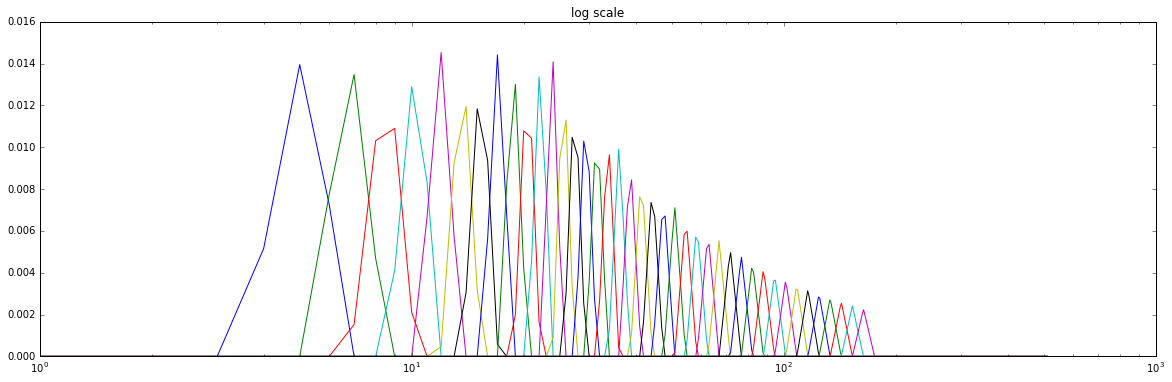
再之後我們會對得到的結果取 magnitude 的平方再取 log ,取 log 之因也是因為人耳對 magnitude 的感知也是 logarithmic (所以分貝的定義才會是$10 \log_{10}(\frac{P}{P_0})$),而更重要的是,透由這個步驟,我們可以在最後一步的 $\Delta$ 操作中,將 noisy channel 的影響給 cancel 掉 (因為在頻譜上其影響是相乘,取 $\log$ 後變相加)
spec = np.abs(fftpack.fft(input,nfft))**2
mel_filter_bank = trfbank(samplingrate,WINDOW_LEN)
melspec = np.log(np.dot(input,mel_filter_bank.T)) # elementwise mul for each filter, then sum it
Remark: 取$\log$ magnitude 平方後,可以看到頻譜上是 symmetric 的 (因為 time domain 上的 real signal 經過 Fourier Transform 之後,在 freq. domain 上是 conjugate symmetric 的 (也就是 $F(b_0) = a + jw$,$F(-b_0) = a - jw$) ,其 magnitude 是一樣的。另外 DCT 上頻譜的週期性,我們有 $F(-b_0) = F(-b_0 + N)$,而 Sampling Theorem 告訴我們,所能 detect 的最大頻率 $f_M$ 為 sampling rate 的一半,否則會有 alias 的現象,對應的頻率出現在頻譜中間)

Remark: 每個 frame 的頻譜上有 $N$ (usually $ N = 512$) 個頻率點,因為在頻率上做操作,所以 經過filter 這個操作,就僅僅是相乘而已。另外,我們會把每個 frame 過特定 filter 的值給 summation 起來,當作該 filter 被這個 frame 所 activate 的量。
IDFT (DCT)
經過 Mel Fiterbank 後,其實對每個 frame 我們已經有了其 feature (dimension = filter 數目),但這些 feature 彼此是互相 correlated 的 (這也很好理解,因為上述的 filterbank 有 overlap 的部份),對於某些機器學習的算法,這是我們所不樂見的 (但詳細是為什麼我還沒有去探究),所以我們想將這些 feature uncorrelate ,而這裡我們使用了 Discrete Cosine Transform。
這篇文章 圖解了一維數據經過 DCT 後所對應的各分量,這麼做的好處在於,因為上述的 feature 包含了 both source 和 filter 的資訊 (直到這裡,我才理解 MFCC 也屬於 Source-Filter model),但對於 unvoiced speech , excitation 只是一堆白噪音,會在頻譜上加上許多密集的 毛 (voiced speech 也是,但因為 pulse train 在 freq. domain 上是 sinc function ,所以這些毛是等間隔的)。
而 DCT 越後面的項代表的是在頻譜上變化越快速的量,也就對應到了 excitation ,所以只 pick 前幾項相當於濾掉了 excitation 的影響!
fftpack.realtransforms.dct(input,norm='ortho')[:,:NUM_CEPS]
Remark: 可能有讀者會以為白噪音僅僅是在描述那些高頻部份的噪音,但我們所說的白噪音在任何頻率上強度都是均勻分佈的。之所以會對高頻部份特別有感,得從耳朵的構造說起,因為耳朵由外到內的 filter 是高頻到低頻,所以低頻部份的白噪音被 activate 的時候,其強度遞減的比較多,所以我們對高頻白噪音才會特別敏感。
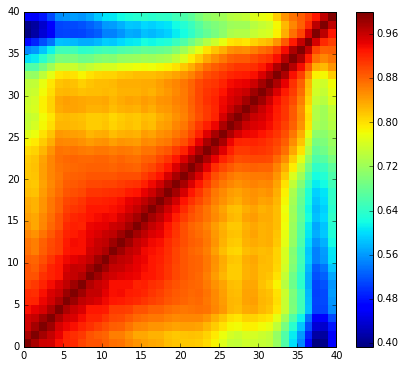
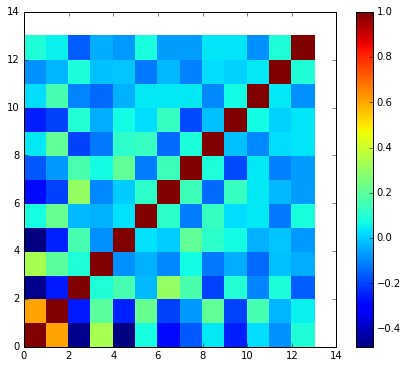
Remark: 照理來說, DCT 作用於 real and even function,但這裡我們直接忽視 phase ,來 extract magnitude 上那些變動的各分量。
Delta Coefficient
為了 catch 聲音訊號的變動,直接求差分效果不好,用 LR 的方法求一次近似的斜率,待補!
comments powered by Disqus