語音辨識的基本架構中,第一步便是要把聲音訊號轉成可被紀錄的數位形式以供 machine 處理。科學家們從人類究竟是如何發出特定聲音作為出發點,去找出訊號當中哪些是屬於那個聲音 unique 的 feature,並移除那些無關的資訊 (e.g noise) ,並利用這些 extract 出來的 feature 來作為辨識的基本元素。
Source-Filter Model
前面講的非常抽象,究竟聲音是如何產生的呢?
透由聲帶的振動,有頻率地送出來自肺部的氣流,這些氣流經由聲道及唇齒舌不同的構造及位置 (vocal tract),發出不同的聲音 (see speech synthesis)
我們用以下的數學模型來描述,視聲帶振動所送出的氣流為聲源 $e[n]$ ,而 vocal tract 則視為一個系統 $H$ ,而兩者之後的 output 即為我們所聽到的聲音 $s[n]$。
Remark: 其實應該要是連續的 $e(t)$,這裡已經做了 sample ,所以是離散的 $e[n]$ 及 $s[n]$
很粗淺的分類: 濁音 vs 清音
濁音 (voiced speech): 發聲時會聲帶會振動的那些音 (母音及部份子音),可以用手摸喉嚨感受看看!
清音 (unvoiced speech): KK 音標中的 [s] ,[ts] ,[f], [p]
Remark: 原本想舉注音符號當例子,但發現都會振動,因為我們的注音符號後面都會跟一個濁音 (像是ㄆ會念成ㄆㄜ,ㄈ會念成ㄈㄜ,ㄊ念成ㄊㄜ),也算是意外的發現呢XD
而聲帶會振動的濁音,是有週期性的送氣到 vocal tract ,而清音則是氣流直接灌進去(類似 white noise ),無週期可言, 而從頻譜上來看,更可以發現當中的一些特性 (以下是我利用 WaveSurfer 所錄製的 「阿斯」(??? )
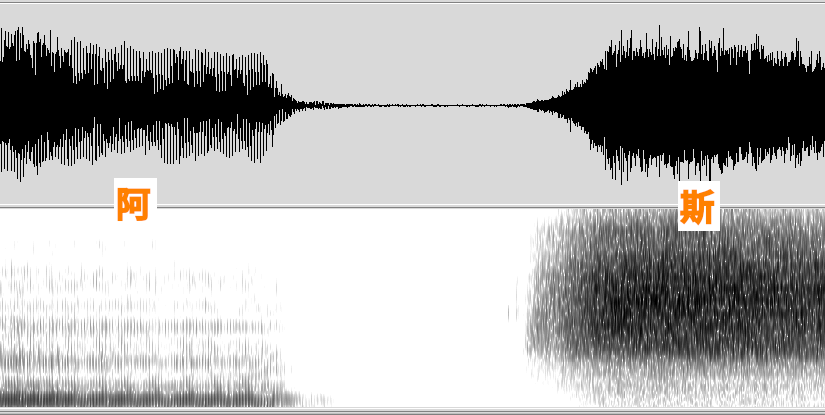
可以發現到濁音在低頻的部份比較強,而清音則是在高頻,解釋是畢竟聲帶的振動頻率有其生理限制,不能發到太高頻的音。
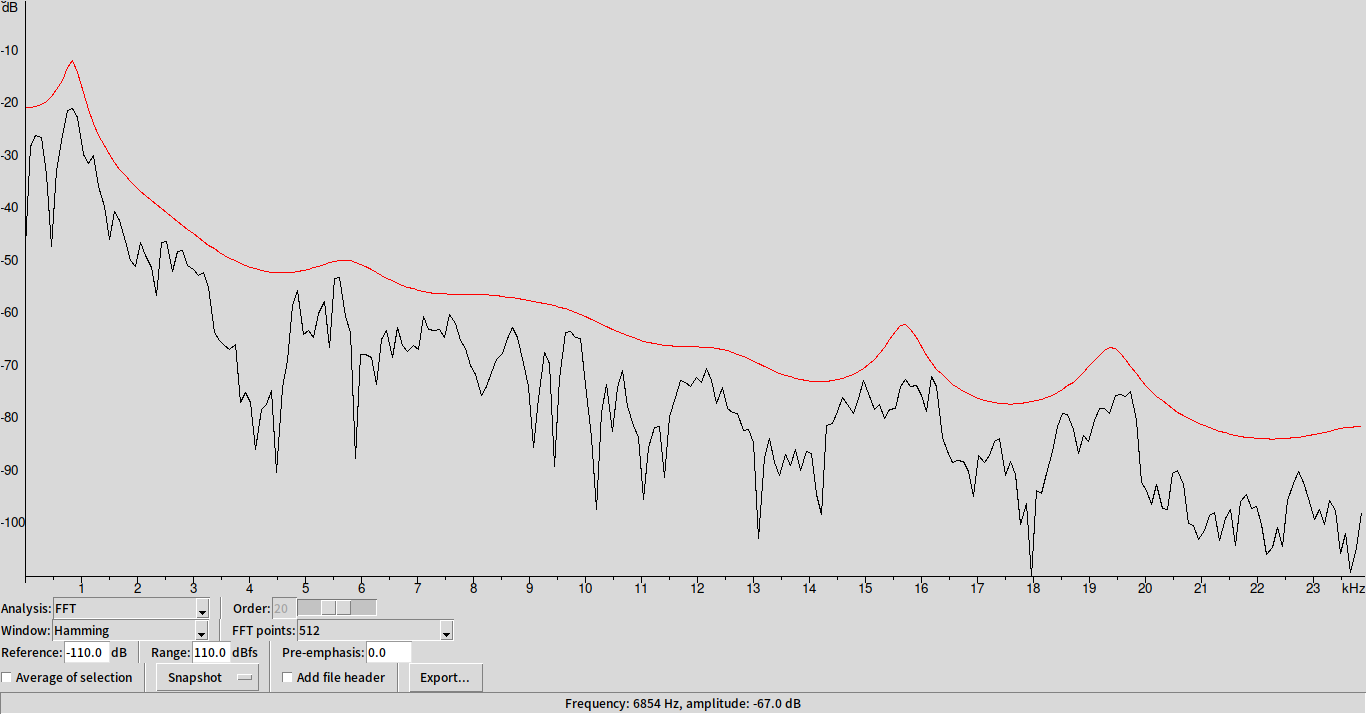
取其中一小個 frame 來看
阿
斯
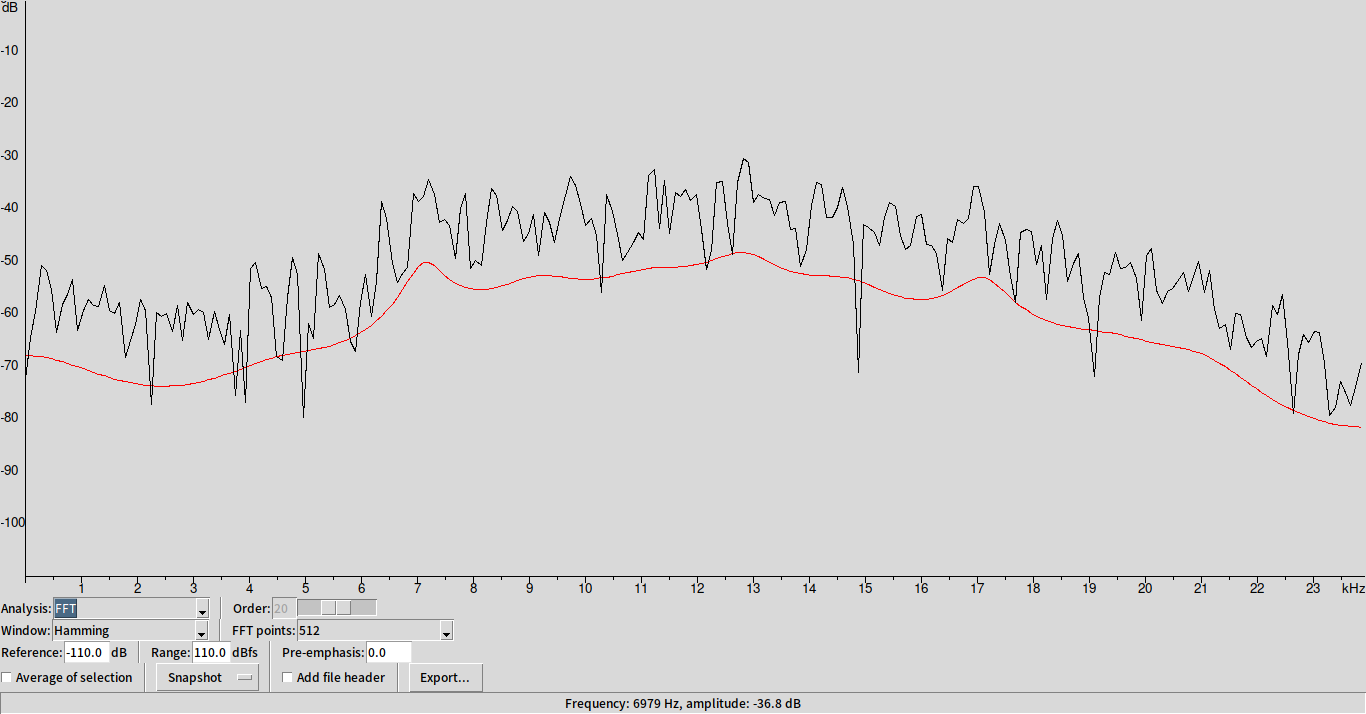
可以發現在紅色線上,有幾個凸起的小 peak ,其中對應的頻率我們稱之為 formant frequency (對應到 $H$ 的 pole ),用來當作描述 vocal tract 的特徵。除此之外,每個人聲帶振動頻率的不同,決定了其音高($F_0$)(可以在 time domain 從濁音的波形看出來)。
發聲示意圖
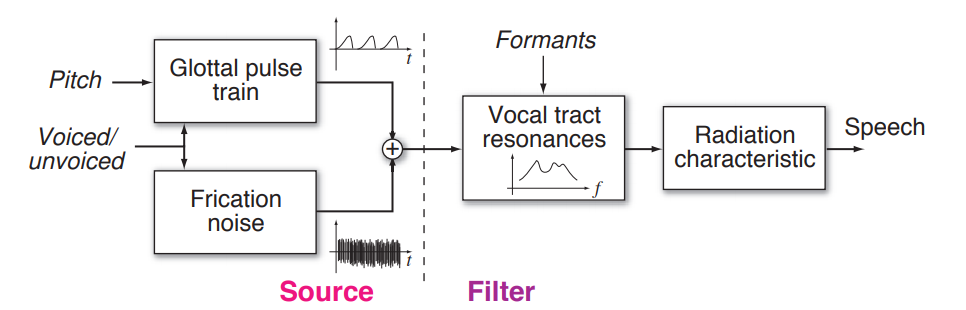
看到這裡,或許你會想說,那麼利用 formant frequency ,可能可以幫我們確定所發的音。事實上也的確如此,聽說有些專家可以看頻譜就知道所對應的語音是在講些什麼,那有什麼方法可以幫我們擷取出這些 frequency 呢?
First attampt - Linear Prediction Coefficient (LPC)
當你打手機時,你有想過你的聲音是怎麼被對方聽到的嗎? 一個最 naive 的作法是將每個時間點 sample 到的值記錄下來,然後 transmit 給對方, 那麼這樣你一秒鐘需要傳多少資料呢?假定 sampling rate 是 8kHz 的話,你需要傳 8K 個資料點。 這 8K 個資料點當中有沒有冗餘的資訊呢?(額…不是指廢話的那種沒有資訊)有沒有辦法傳更少,但卻同時保有一定的音質?
因為人的生理構造限制,我們沒有辦法很快的改變我們的唇齒舌之位置,也就是說相鄰的音之變化是連續的,而剛剛提到唇齒舌位置可以視作是一個系統 $H$ ,而這也表示這個系統當中的參數之變化,會持續一段時間,不會馬上變化 (相較於我們的音高在 80 ~ 1kHz之間,其相對變化得很慢,約在50 ~ 100 Hz 之間),所以如果我們不是記 time domain 上快速變化的聲音訊號,而是變動相對緩慢的系統參數,便可以不用計那麼多的資料點。
Basic of LPC
這裡所介紹的 LPC ,假定當前時間點的訊號值 $s[n]$ 由聲帶送出的氣流 $e[n]$ 及先前時間點的訊號 $s[n-k]$ 所決定。
$$
s[n] = \sum_{k=1}^{p}a_ks[n-k] + e[n]
$$
所對應的系統就是
$$
H(z) = \frac{S(z)}{E(z)} = \frac{1}{1-\sum_{k=1}^{p}a_k z^{-k}} = \frac{1}{A(z)}
$$
這裡假定了該系統並沒有 zero 的存在,而是由 formant freq. 對應的 poles 所構成。
Remark:
- 這裡的 $e[n]$ 又被稱為 excitation, prediction error, residual signal
- 求 {$a_k$} 的方法是利用 minimize $\sum_n e^2[n]$ 去求解對應的係數 (雖然 $e[n]$ 其實不能算是 error 啦…)
Experiment of LPC
一個有趣的問題是,我們可以只記 $H$ 的參數 {$a_k$}嗎?
正常來說,我們要將 $s[n]$ 給反濾波出來($E(z) = A(z)S(z)$),得到 $e[n]$(會很像 white noise) ,並去 track 這個 $e[n]$ 的音高 (simple pitch tracker)才能得到比較好的音質。
在這個 repo 裡中的 ipynb 裡,有一些小實驗,當中 lpc 相關函數,是來自 Columbia 的 ELEN E4896,另外,我做了一些小修改,使它可以用 python3 跑。
另外,一個值得思考的問題是 $p$ 該取多少比較好?對 $8$ kHz sampling rate 的音訊來說,取個 8 - 12 差不多,取太大的 $p$ 結果反而不好 (實驗結果 recover 回來會像在水底說話的咕嚕咕嚕音),我的解釋是 LPC 想 model 的是 filter ,但如果 $p$ 取的太大,會連 source 都 model 進去 (OVERFITTING! model is too powerful!),但這個模型的假設就是 source 和 filter 彼此是 independent 的 (而且對 unvoiced speech , source 基本上就是 white noise) , model 到 white noise 會慘掉也是不意外。
Remark: 很多機器學習的 model 在 training 時都會有一樣的問題,雖然我們假設有一個 ground truth 的函數 $f^\star(x)$ 去 generate 出 sample ,但實際上在觀測時,所看到的 $f(x)$ 都會被雜訊覆蓋,但基本假設是 $f^\star(x)$ 和雜訊是獨立的,而我們想從 training data 中萃取出 $f^\star (x)$ ,但如果你用了太強的 model ,連雜訊都一併 model 進來的話,在 testing 時, performance 反而會壞掉…
所以跟語音辨識到底有什麼關係?
既然我們可以利用這組參數去 rebuild 出原先的聲音訊號,那麼就代表這組參數蘊含了語音當中對辨識來說重要的資訊,拿來當作 feature 比起直接拿整個頻譜餵給我們的 ASR 來的有效率多了!(類似的概念在訓練 autoencoder 也常常用到,或者像 word2vec 當中拿 bottleneck layer 作為 distributed embedding 也是一例)
