在前幾講的討論中,我們討論了 binary classification 的問題,及這個問題在機器學習上的可行性。但很多時候,我們不希望機器只會說是或不是,亦即不希望它的 output space $\mathcal{Y}$ 只是單純的 {$1, -1$}。舉例來說,給定一些資料,請你預測明天的股價,除了想預測會漲或會跌之外,到底漲多少或跌多少也是我們有興趣知道的事情,而這也是接下來兩講想解決的事情 - Regression。
Basic
想像我們今天有一把 data $\mathcal{D}$,其中的每一筆為 ($\mathbf{x},y$)的 pair,其中 $x \in \mathbb{R}^d, y \in \mathbb{R}$。之前的 binary classification 做的事情就是在 $\mathcal{R}^d$中找 hyper-plane 去將空間一分為二,而 regression 所做的事也是嘗試去找到這樣的一個 hyper-plane,同時去 minimize $\mathcal{D}$ 上的每個點到其的距離 (e.g Euclidean distance)。
Feasibility of Learning
Sufficient small $E_{in}$
上面提到的距離就是所謂 error。
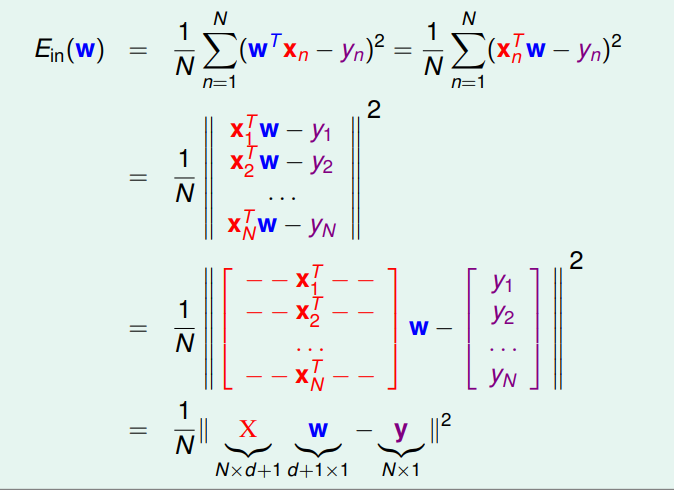
可以看出 $E_i$ 是 convex function,可以透由找 $\nabla_w E_i = 0$所對應的點找到我們要的 weight。
在 linear regression 中,這樣的 weight $\mathbf{w}_{\text{LIN}}$ 是有 closed form 的。
從幾何的觀點來看,就是 $\mathbf{y} \notin $ col $(X)$ ,亦即 找不到一個 $\mathbf{w}$ 滿足 $X \mathbf{w} = \mathbf{y}$,所以退而求其次,將 $\mathbf{y}$ 投影到 col($X$) 上 (which is $\underset{\text{projection}, P}{\underbrace{X(X^TX)^{-1}X^T}} \mathbf{y}$),再去找出對應的 $\mathbf{w}$ ,也就是上方的 $\mathbf{w}_{\text{LIN}}$。
Generalization to $E_{out}$
回顧 binary classification,Out-sample 的 error 會被以下 bound 住
$$ E_{out}(f) = E_{in}(f) + \mathcal{O}(\sqrt{\frac{d_{VC} \, \ln N}{N}}) $$
對於 Regression 問題,我們還先要定義 $d_{VC}$ 是什麼,以及所對應的 generalization bound。
關於 $d_{VC}$ , 原先的定義似乎不太適用,我們沒辦法定義在 $\mathbb{R}$ 上的 **shatter** 究竟是怎麼一回事,但從自由度的觀點來看,有跟 linear preceptron 一樣的 dim 是很直覺的(就只是經過了 step 變換而已) (似乎有個叫 psuedo dimension 的主題就是將其推廣至 regression ,這裡就不繼續探討了)
先來回想一下,當初 classification 的 generalization bound 是怎麼 derive 的,假設資料是線性可分,我們在空間中 sample $N$ 點,以此去找出可以將空間一分為二的最佳平面 (dichotomy) ,但因為我們只能 sample 有限的點,對沒 sample 到的那些,可以總是有個小惡魔做出跟我們相反的決策 claim 我們是錯的,而我們利用 Hoeffeding Equality 以及 hypothesis set 的幾何特性去說 $E_i$ 跟 $E_o$ 相去甚遠的機率很小。而如果有 flipping noise 的話,找 $f(\mathbf{x})$ 則變成找 $f(\mathbf{x}, y)$ 的 joint dist.
而今天在 Linear Regression,我們對資料的假設又更強了,假設今天有個 oracle 說,已知所有在 $\mathbb{R}^3$ 中的 data 都落於一個二維平面上 (對應到 classification 線性可分的條件),那麼我們跑 LR 所得到的結果,無論在 training 還是testing , error 都是完美的 $0$ (其實在這種情況下,跑個反矩陣運算就解決了…)。
所以這裡引進 noise 的討論就重要了(在後面會提到,除了隨機的雜訊外 (white noise 的概念),今天 ground truth model 過於複雜使得 hypothesis set 無法完整 catch 所造成的誤差,也是 noise 的一種,所以我們必須 model ,畢竟我們其實沒有 oracle XD)。\
我們假定 $y = \mathbf{w^\star}^{T} \mathbf{x} + \epsilon$,而這個 $\epsilon$ 會讓資料開始從平面上跳走,幾何上來看就是加入了垂直於 col(${X})$ 的分量。 (Note: 這裡把投影到 col($X$) 的 矩陣特稱為 Hat matrix $H$)。
則 $E_i$ 可以看成是 Noise $\tilde{\mathbf{n}}$ 投影到 Null($X$) 的分量,which is $(I-H) \mathbf{y}$ \
以下是圖解
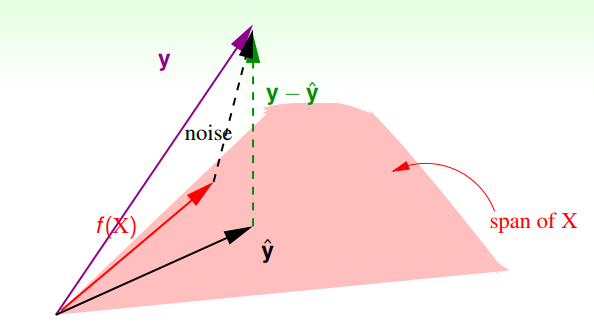
$$ E_{in} = \frac{1}{N}||\mathbf{y} - \mathbf{\hat{y}}||^2 = \frac{1}{N}||(I-H) \tilde{\mathbf{n}}||^2 $$
Lemma: trace($AB$) = trace($BA$)
Lemma: trace($H$) = $d+1$, Assume $X^TX$ is invertible\
(白話來講就是他的 col. vector 們是 linear independent),故其 dim. 為 $d+1$
proof:\
trace($H$) = trace($X(X^TX)^{-1}X^T$) =
trace($(X^TX)^{-1}X^TX$) = trace($I$) = $d+1$
Lemma
$$ \boxed{E_{in} = \frac{1}{N}||(I-H) \mathbf{\tilde{n}}||^2 = \frac{1}{N}(N-(d+1))||\mathbf{\tilde{n}}||^2} $$
proof:
$||(I-H)\mathbf{\tilde{n}}||^2 = \mathbf{\tilde{n}^T}(I-H)^T(I-H)\mathbf{\tilde{n}}$ \
因為 $(I-H)$ 也是個投影矩陣,所以我們有其 symmetric 及冪等性兩個性質,\
所以 $= \mathbf{\tilde{n}^T}(I-H)\mathbf{\tilde{n}}$,
結果為一個值,故亦等於其 trace,用跡數相乘的可交換性,我們可以得到
$E_i$
再稍微推導一下, $E_o$ 可以得到類似的式子 (但證明我看不懂了QQ)
$$ \boxed{E_o = \text{noise level} \cdot (1 + \frac{d+1}{N})} $$
所以 Generalization bound 可以寫成以下 (Assume Noise level is constant)
$$ E_{out}(f) = E_{in}(f) + \mathcal{O}(\frac{d_{VC}}{N}) $$
