在此之前,針對 linear separable 的 data ,我們利用找可以切分這些數據點的 hyper-plane 來做 classification (或 regression )。但這個強大的假設並不適用於每筆真實世界中的 data ,所以我們勢必得處理 non-linear 的問題。換句話說,我們希望 hypothesis set 中可以包含更多的候選人(可以 match nonlinear 特性的那些 function ),同時去驗證在這樣的情況下,學習依然是可行的。
Feature Transform
既然 linear function 不夠用,一個很直觀的想法是引進更高 order 的函數。
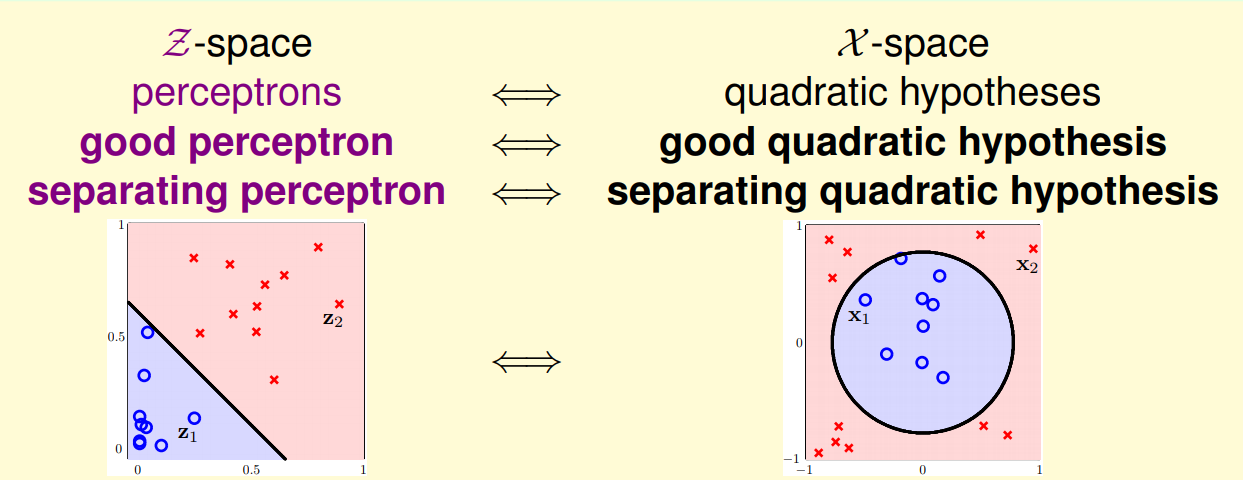
上面那個例子中,展示了 circular data 的分類問題,如果只取 $x_1, x_2$ 無法 separate ,但如果多考慮 $x_1^2, x_2^2$ 便能成功 (而且依然能處理原先 linear separable 的 data , i.e 退化的情形同時可以考慮,亦即 $\mathcal{H}\scriptsize old \normalsize \subset \mathcal{H} \scriptsize new$)。
從另一個角度看,相當於是我們將 data 做了 feature transform ($\phi(\mathbf{x})$) 到新的空間,而在這個空間中,其是 linear separable 的。\
e.g General Quadratic Hypothesis Set
$$ \mathbf{x} \in \mathbb{R}^2 \stackrel{\phi}{\longmapsto} \mathbf{z} \in \mathbb{R}^6 $$
$$ \text{其中}\quad \phi(\mathbf{x}) = (1,x_1,x_2,x_1^2,x_2^2,x_1x_2) $$
而在新的 space 中,因資料滿足了 linear separable 的特性,前幾講討論的方法都可以適用。而在這個 space 中找到一個好的 hyper-plane ,相當於在原資料中找到好的 quadratic plane。
Feasibility of Learning
前方曾經提過,model complexity 雖然能 minimize 在 training data 上的 error ,使 得 hypothesis function fit data 的程度越好,但相對應的代價是不太能做 generalization (後面會提到,這就是 overfitting 原因的其中一種)。
而衡量這些代價,可以從在新空間中 hyper-plane 的 VC dimension 去想。\
對一般 $Q \scriptsize th$ order 的 POLY transform ,$d \scriptsize \text{vc}$ 為 $H_Q^{d+1}$ ($\mathbf{x} \in \mathbb{R}^d$),複雜度依 $\mathcal{O}(Q^d)$ 上升。

Remark: 實務上都先從最簡單的 linear model 開始,再去逐步增加 model complexity ,並利用 validation set 找出最適合的維度
