Linear Model 的核心在於 feature 分量的 weighted sum $\mathbf{w}^T \mathbf{x}$, 在 binary classification ,我們用 step function 將其二分 ($\mathcal{Y} = \lbrace , -1,1,\rbrace$),而在 linear regression 中,我們將其直接作為輸出。而這一講要介紹的則是將 $\mathbf{w}^T \mathbf{x}$ 通過一個 nonlinear function mapping 到[$0,1$],賦予他機率的意義 ($\Pr[y = +1 | \mathbf{x}]$)。
Logistic Function
$$ h(\mathbf{x}) = \theta(\mathbf{w}^T \mathbf{x}), \quad \theta(s) = \frac{e^s}{1+e^s} $$
一個 step function 的 soft 版本。
Error Measure
而正常來說,我們所擁有的資料,並不是 feature 對 probability 的 pair ,而是跟binary classification 一樣的資料,也就是說 data 是由以下的 target 產生。
$$ \Pr[y|\mathbf{x}] = \begin{cases} f(x) \;&, y = +1\\ 1-f(x) \; &, y = -1 \end{cases} $$
所以接下來的問題是,我們想優化的 $h(x)$ 跟 $f(x)$ 有什麼關係。 給定一組 data $\mathcal D = \lbrace (\mathbf{x}_1,+1),\cdots,(\mathbf{x}_N,-1) \rbrace$,我們可以算它被產生的機率有多少,而既然他會被我們 sample 到,代表機率一定不小,同樣地,如果 $h(x)$ 學得好的話, behavior 要跟 $f(\mathbf{x})$ 差不多,所以我們不妨考慮由 $h(x)$ 去 generate $\mathcal{D}$ 的可能性(likelihood),並去 maximize 它 (表示其跟 $f(x)$ 越像)。
logistic 函數有一個性質是 $\theta(-x) = 1 - \theta(x)$,所以上方所講的 likelihood 可以表示成以下,
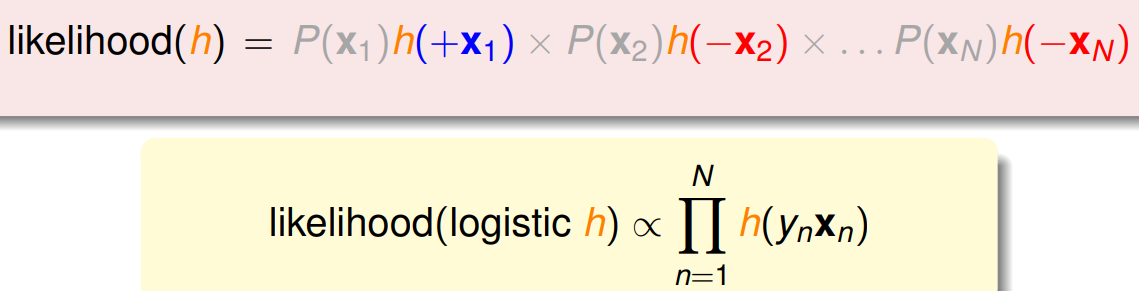
Maximize likelihood 等價於 minimize 以下,
$$ \frac{1}{N} \sum_n \ln(\frac{1}{\theta(y_n\mathbf{w}^T\mathbf{x}_n)}) $$
定義 $E_{in}$ 為
$$ \boxed{E_{in} = \sum_n \underbrace{\ln(1 + \exp(-y_n \mathbf{w}^T \mathbf{x}_n))}_{\text{cross-entropy error}}} $$
Feasibility of Learning
Sufficient small $E_{in}$
可以證明$E_i(\mathbf{w})$ 是 convex,代表可以用 $\nabla_w E_i(\mathbf{w}) = 0$ 來找到 weight $\mathbf{w}^\star$。
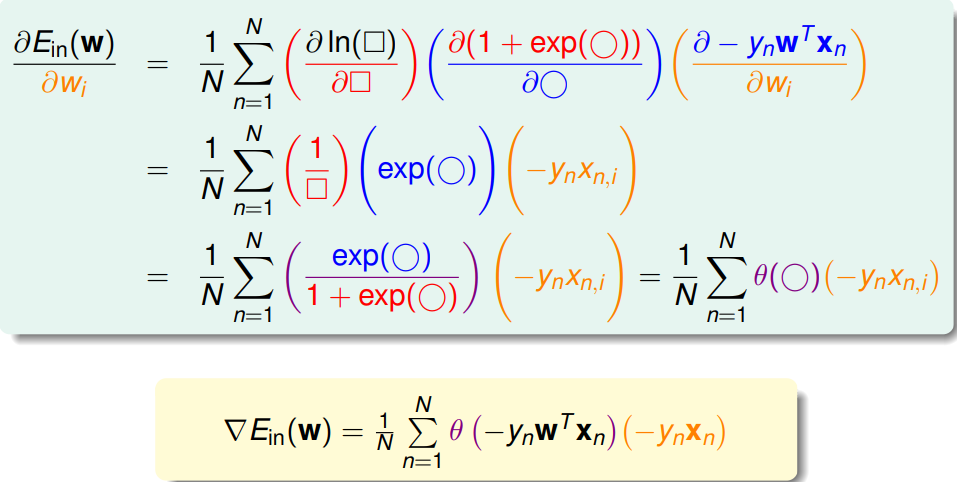
但跟在 linear regression 不同的是,這裡 $\mathbf{w}$ 被包在 $\theta(\cdot)$ 裡頭,而非單純的線性組合,不存在 closed form 的解可以一步到位。
那我們該怎麼優化 $\mathbf{w}$呢?
一個 iterative 的方法是,去 check $\mathbf{w}$ 周圍的點 $\mathbf{w}^\prime$,看是否能得到更好的結果,如果可以的話,就移至該點並重複此步驟,直到附近的點都不會再有更好的結果為止,便可以說我們走到了 local optimal (谷底的概念)。
Remark: 之後會證明這個 local optimal (對於 convex 的 $E\scriptstyle in$而言),就是 global optimal
所以如何找到下一步要移動的點呢?
Gradient Descent
在這裡我們使用 Gradient Descent。
想法是利用 Taylor Expansion 的一次近似,為了簡單討論,我們先固定在以該點為圓心,半徑 $\eta$ 的圓上找(目前先 care 方向),有以下 approx. ( $|\mathbf{v}^T\nabla E_{in}| = 1$)
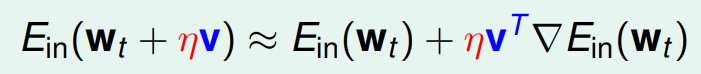
會有最好結果的鄰居,方向剛好在 $\nabla E_{in}$ 的反方。
$$ \mathbf{w}_{t+1} \leftarrow \mathbf{w}_t - \eta \frac{\nabla E_{in}(\mathbf{w}_t)}{||\nabla E_{in}(\mathbf{w}_t)||} $$
那 $\eta$ 這個 hyper-param 怎麼選呢?
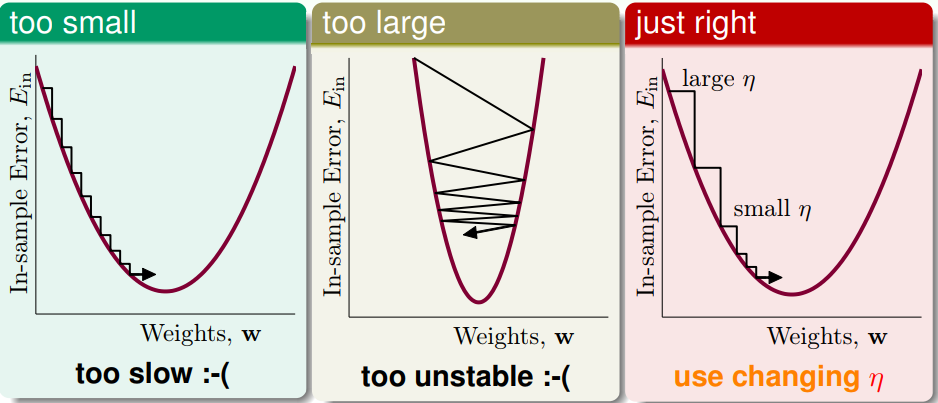
我們的更新式採用了右邊的 changing $\eta$
$$ \mathbf{w}_{t+1} \leftarrow \mathbf{w}_t - \eta \nabla E_{in}(\mathbf{w}_t) $$
Remark: $||\nabla E_i||$ 包含了每次 step 大小的資訊,在陡峭的地方,我們一次順勢滑落比較多,而當趨於平緩時,則減小步伐。
Remark: 如果跑了 $D$ 輪,時間複雜度為 $\mathcal{O}(ND)$,不保證找到最佳解(雖然知道谷底存在,但不一定在 $D$ 輪可以走到)。
Global Optimal 保證
假設我們得到的 local optimal weight 是 $\mathbf{w}_l$,假定存在某一點 $\mathbf{w}_g$ , $\mathbf{w}_l \not = \mathbf{w}_g$ ,使得 $E_i(\mathbf{w}_g) < E_i(\mathbf{w}_l)$
因 $\mathbf{w}_l$ 是 local optimal ,代表存在一個 neighborhood 集合 $U$ ,其中 $\forall \mathbf{w}_z \in U$ , $E_i(\mathbf{w}_l) < E_i(\mathbf{w}_z)$
考慮 $\tilde{\mathbf{w}}_z = c(\mathbf{w}_l) + (1-c)(\mathbf{w}_g) \in U$, $0 < c < 1$\
(概念上就是在 $\mathbf{w}_l$ 跟 $\mathbf{w}_g$ 之間連一條線,並找 $\mathbf{w}_l$ 的 neighborhood)
又因 $E_{in}$ 為 convex ,所以
$$ \begin{aligned} E_{in}(\mathbf{w}_l) &< E_{in}(\tilde{\mathbf{w}}_z)\\ &= E_{in}(c(\mathbf{w}_l) + (1-c)(\mathbf{w}_g))\\ &\leq c E_{in}(\mathbf{w}_l) + (1-c) E_{in}(\mathbf{w}_g) \end{aligned} $$
$$ \require{cancel} \implies \cancel{(1-c)} E_{in}(\mathbf{w}_l) < \cancel{(1-c)} E_{in}(\mathbf{w}_g) \quad \Rightarrow\Leftarrow $$
Generalization to $E_{out}$
待補
