最近開始刷 LeetCode 練習思考,這題討論串的某個解法蠻神的,因此來紀錄一下。
題目敘述
Given an array nums containing n + 1 integers where each integer $\in [1,n]$, Assume that there is only one duplicate number (but can be repeated many times), find the duplicate one.
限制
- You must not modify the array (assume the array is read only).
- You must use only constant, O(1) extra space.
- Your runtime complexity should be less than $O(n^2)$.
O(n) 簡單算法 (W/ modifying array)
與 LeetCode448 - FindDisappearedNumber一樣,在保有原先 array 資訊的情況下立 Flag。
int findDuplicate(vector<int>& nums) {
for(size_t i=0;i<nums.size();++i){
if(nums[abs(nums[i])-1] < 0) return abs(nums[i]);
else nums[abs(nums[i])-1] *= -1;
}
}
簡單!但是不合題目要求XD
(如果沒加 read-only 這個條件,只說跑完該 function ,array 不能變其實可以用,反正
就再跑個一輪加 abs() 😛)
O(n $log$ n) - 利用鴿籠原理的想法
看到題目限 $O(n^2)$ 複雜度,可以想到二分搜或排序,但不能開另外的 container ,所以應該是二分搜。
每次都砍半,去 check [1,mid] 中 element 的個數,如果比 mid 還大,代表裡頭有重
複,反之就是另一個沒被檢查到的區間,每次都要 iterate 一輪,但 $O(\log N)$ 輪便可找到答案。 (我想這題被放在 medium 應該是因為存在這個簡單的算法XD)
int findDuplicate(vector<int>& nums){
int low = 1,high = nums.size()-1;
int mid,cnt;
while(low <= high){
cnt = 0;
mid = (low + high) /2;
for(auto n: nums){
if(n <= mid) ++cnt;
}
if(cnt <= mid) low = mid +1;
else high = mid - 1;
}
return low;
}
O(n) - Tortoise and Hare Algorithm
沒寫過當場想的出來真的是大神…\
In Brief,觀察到區間是 $[1,n]$,且沒有缺漏的元素,在不存在重複元
素的情況下, index 與 value ,可以想成 $[1,n] \mapsto [1,n]$ (Permutation!),
所以 nums[0], nums[nums[0]], nums[nums[nums[0]]]… 可以把元素都 iterate
一遍,也就是一個 path。
好!但今天我們確定有一個(也是唯一一個)元素重複了,對這個性質會造成什麼影響呢?
WLOG,我們從眾多可能 permutation 挑出一個最好思考的(照順序的),已知今天是有 $n+1$ 個元素,假定我們今天在 $[1,n]$ 的最後接上$[1,n]$中的任一個值,如以下紅色部份
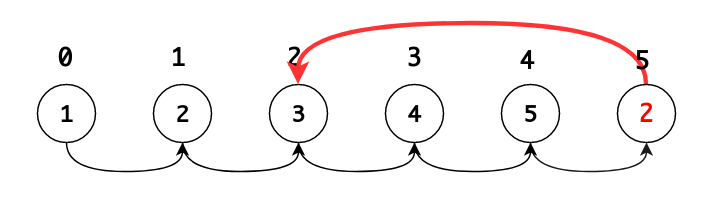
會將原先一條依序 iterate 過所有元素的 path ,變成一個 path 與 cycle 的 混合路徑(?)。因為 $0$ 不存在元素裡頭,所以首位元素為一個 source。 由此可確定這個路徑中至少有一單位長度的 path 。
過來是這個演算法精華的部份,如以下示意圖,重複的元素為 path 進入 cycle 的 entry point (注意到根本輪不到第三個重複元素,兩個就會形成cycle) ,那該如何偵測呢?
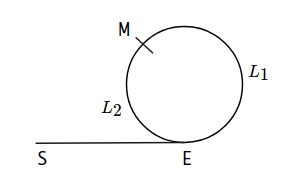
maintain 兩個 pointer,其中一個(hare)一次走兩步 (i.e nums[nums[i]]),另一個(turtle)一次走一
步(e.g nums[i]),因為迴圈存在,步數公因數又為 $1$ 所以最後一定會
相遇於 cycle 上一點 $M$,這點具有什麼特性? 整理下我們有的式子。
$$ 2\times (\underbrace{n_1 C + L_1 + \overline{SE}}_{turtle 走的長度}) = \underbrace{n_2 C+L_1 + \overline{SE}}_{hare 走的長度} $$
移項可得
$$ L_1 + \overline{SE} = (n_2 - 2n_1)C = nC, \quad n \in \mathbb{N} $$
-
$n = 1$, $\overline{SE} = L_2$,令兩個 pointer 分別從 M 和起始點出發(但這次步伐相同!),交會點即是 $E$ 。
-
$n = k$, $\overline{SE} = (k-1)C + L_2$,與上面一樣,會 發現交會點亦是 $E$ 。
int findDuplicate(vector<int>& nums)
{
int t = nums[0];
int h = nums[nums[0]];
while (t != h){
t = nums[t];
h = nums[nums[h]];
}
h = 0;
while (t != h){
t = nums[t];
h = nums[h];
}
return t;
}
很精闢的演算法!
comments powered by Disqus