前一講中講述了 break point 的存在,壓制了 growth function $m_H(N)$ 的成長速度,於這一講中,我們想嚴格地說明只要存在 break point ,$m_H(N)$ 便會是 POLY(N) 。
Bounding function $B(N,k)$
為了方便討論各種不同的 hypothesis set ,我們僅利用 break point 去描述一個 hypothesis set (做點分群這樣。),而 $B(N,k)$ 為其 upper bound ,表示在 $N$ 筆資料點中,任意 $k$ 個點不能被 shatter 的條件下, dichotomies set size $m_H(N)$ 最大能為多少。
而現在我們要來填 $B(N,k)$ 這個 table ,從中找一些規律幫助我們證明 $B(N,k) \in , \mathbf{POLY}$。
Trivial case
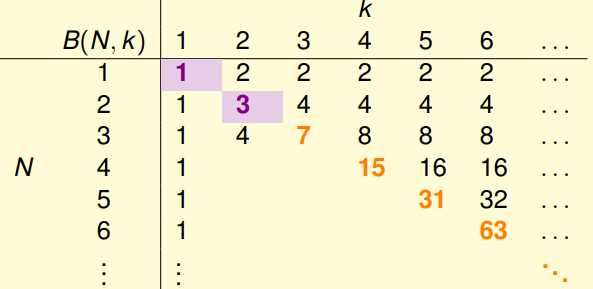
- when $k = 1$, $B(N,1) = 1$
- when $N < k$, $B(N,k) = 2^N$ (the break point condition is useless)
- when $N = k$, $B(N,k) = 2^N - 1$ (just remove arbitary 1 dichotomy)
Inductive case N > k
就像 DP 在做的事情,我們希望能透由前方的 entry (e.g $B(N-1,?), B(?,k-1)$ 去連結 $B(N,k)$)。\
舉 $B(4,3)$ 為例,我們可以找到一組 size 最大的 dichotomies set $\mathcal{H}(\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_N)$,並對它根據 $\mathbf{x}_1 \sim \mathbf{x}_3$是否成對出現做分類,如以下:

並分別令 $2\alpha, \beta$ 為其 dichotomy 的數量
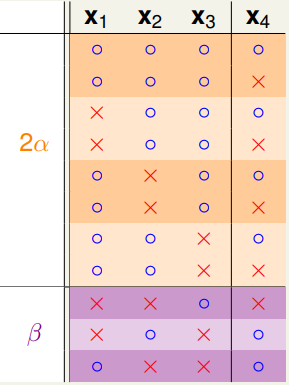
對此分成兩種 case 討論:
Case1: 僅看 $\mathbf{x}_1 \sim \mathbf{x}_3$,重複出現的只看一 遍,根據 任意 $k$ 點不能被 shatter 這個條件,我們知道 $\alpha
- \beta \leq B(3,3)$ (或者說 $\textcolor{orange}{B(N-1,k)}$)。
Case2: 看那些 $\mathbf{x}_1 \sim \mathbf{x}_3$ 成對出現的 dichotomies ,其 $\mathbf{x}_4$ 必是一正一反,是故在 $\mathbf{x}_1 \sim \mathbf{x}_3$ 中,不能有任意 $k-1$ 個點可被 shatter (否則搭配 $\mathbf{x}_4$ , $k$ 個點便可被 shatter 了)。所以有 $\alpha < B(3,2)$ (亦即 $\textcolor{purple}{B(N-1,k-1)}$)
綜合以上,得到 $B(4,3) = \textcolor{orange}{ \alpha + \beta} + \textcolor{purple}{\alpha} \leq \textcolor{orange}{B(3,3)} + \textcolor{purple}{B(3,2)}$
Sauer's Lemma
$$ B(N,k) \leq \sum_{i=0}^{k-1} \binom{N}{i} $$
proof: 用數學歸納法簡單可證
而據此,只要 break point $k$存在,我們便有
Lemma
proof:
先證 $B(N,k) \geq \sum_{i=0}^{k-1} \binom{N}{i}$,
首先構造一個 任意 $k$ 點不被 shattered 的 dichotomies set,\
把 $B(N,k)$ summation 拆開,可以寫為 $\binom{N}{0} + \binom{N}{1} + \cdots + \binom{N}{k-1}$,分別代表了將 label x assign 到 $i$ 個數據點的可能 (對應到一種 dichotomy),而根據這樣的構造方式,沒有一個 dichotomy 會將 $k$ 個數據點都 label 成 x (至多 $k-1$),而若想 shatter $k$ 個數據點的話,我們需要有它們 o, x 的各種組合 (但今天全 x 的不存在),所以如此的 dichotomies set 滿足限制,當然或許可以再增加新的 dichotomy (但根據前個部份的討論,也是知道不行啦XD),總之我們證明了以下敘述正確
Vapnik-Chervonenkis (VC) bound
when $\textcolor{red}{\text{N is large enough}}$
Step1: Replace $E_o$ by $E_i^{\prime}$
詳細的證明我還是有看沒有懂😅 …\
要如此做的精神在於 $E_i(h)$ 可能的值,只有 $m_H(N)$ 個,但 $E_o(h)$ 的值卻有無限個,而這不利於後續的分析,所以我們以跟 sample $\mathcal{D}$ 時一樣的 distribution 去 sample 出新的 $N$ 個數據點 $\mathcal{D}^{\prime}$,作為 validation data (有限個),以 $h$ 在其上的表現 $E_i^{\prime}(h)$ 來 estimate $h$ 在未知 data 上的表現 $E_o(h)$ 。
簡單來說就是,我們想利用 $|E_i(h) - E_i^{\prime}(h)|$ 很大的機率去bound 住 $|E_i(h) - E_o(h)|$很大的機率
Given $h$ ,當 $N$ 很大的時候, $E_i(h)$及 $E_i^{\prime}(h)$ $\sim \mathcal{N}(E_o(h),1)$
我想等價於給定兩個常態分佈 $X,Y \sim \mathcal{N}(0,1)$ ,想問 $\Pr[|X-Y| > \epsilon]$ 的一些不等式,以 $\Pr[|X| > c \cdot \epsilon]$ 表示 之。
Step2: Decompose $\mathcal{H}$ by kind
承 step1,我們現在的 dichotomies 是作用在 $\textcolor{blue}{2}N$ 個 數據點上 (無論 $h$ 是踩到 training 還是 validation data 的雷,都算是 BAD)
Step3: Use Hoeffding w/o replacement
Hoeffding Ineq. 亦會給出與W/ replacement 相同的結果,但現在我們可以算出那個平均錯誤率 $\mu$ 到底為多少,就是 $E_i, E_i^{\prime}$ 的平均, 所以稍微改動一下Step1 得到的式子
