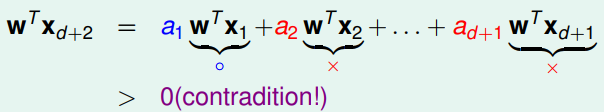於前一講中,我們證明了 growth function 為 POLY(N) iff break point 存在,而這件事可以說明在 training data 上的表現不會和 testing data 差的太多 $E_i(h) \approx E_o(h)$ (if 數據點夠多 $N$ )。而這一講中,我們由 break point 引進 VC Dimension $d \scriptscriptstyle VC$ ,來當作衡量 $\mathcal{H}$ 複雜度的一個指標。
VC Dimension
其實就是 (minimum) break point $k$ 的前一點罷了。
General PLA (w/ higher dimension $d$)
$$
\boxed{d_{VC} = d + 1}
$$
proof:
- $d \scriptscriptstyle VC$ $\geq d + 1$:
That is, for hypothesis $\mathcal{H}$, $\exists$ some $d+1$ 個數據點 can be shattered,所以我們就構造一組這樣的 $\mathcal{D}$ 就可以得證了!
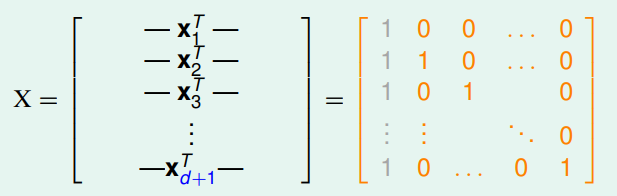
一個可以選擇的數據是在原點及單位正交基底向量 (簡單起見,選擇 $\mathbf{e}_i$) (會這樣想,可以回到第五講中提到,那些退化的 case 反而是不能被 shatter 的特例,所以我們應該是要找能展出整個 input space 的基底才是)
而 shatter 表示什麼呢?表示 given 一組任意的 label $\mathbf{y}$,我們都能找到一組係數與 $X$ 乘一乘後得到它。
因為 $\det(X) = 1$,所以其 invertible !
- $d \scriptscriptstyle VC$ $\leq d + 1$:
That is, for hypothesis $\mathcal{H}$, $\forall d+2$ 個數據點都不能被 shatter 。
而這裡的想法是利用反證法,一樣構造一組 $d+2$ 個 row 的資料矩陣 $X$ ,先假設存在一組 $\mathbf{w}$ 滿足我們所給定的 label assignment。
但因為null($X$) $\not = 0$,所以最後一筆數據不能完全隨心所欲的 assign ,而是 depend on 前 $d+1$ 個,而正是利用此矛盾點,在最後加入一個使得整筆資料不能被 shatter 的老鼠屎 (從 2D 的例子來看,就是找出會讓資料們變成線性不可分的點,在更高維也是),便能得證!
Exploiting Linear dependence
Assume the labels for previous $d+1$ points are $\lbrace \textcolor{blue}{\texttt{o}},\textcolor{red}{\texttt{x}},\cdots,\textcolor{red}{\texttt{x}} \rbrace$
$$ \mathbf{x}_{d+2} = \color{blue}{a_1}\mathbf{x}_1 + \color{red}{a_2}\mathbf{x_2} + \cdots + \color{red}{a_{d+1}}\mathbf{x}_{d+1} $$Then, multiply by $\mathbf{w}^T$, we can find contradiction if the label for $\mathbf{x} \scriptscriptstyle d+2$ is $\textcolor{red}{\texttt{x}}$
Interpretation of VC Dimension
- Effective Degree of Freedom ($\approx$ number of free params)
- Model Complexity
We can rewrite the VC Bound as follows

$\textcolor{purple}{\text{with prob.} \, \geq 1 - \delta }$, The error tolerance $\epsilon$ will be
$$
\sqrt{\frac{8}{N}\ln(\frac{4 \, (2N)^{d_{VC}}}{\color{purple}{\delta}})}
$$
And we also call it penalty for model complexity $\Omega(N,\mathcal{H},\delta)$
$$
\boxed{E_o(g) \leq E_i(g) + \underset{\color{red}{\Omega(N,\mathcal{H},\delta)}}{\underbrace{\sqrt{\frac{8}{N}\ln(\frac{4 \, (2N)^{d_{VC}}}{\delta})}}}}
$$
Conclusion: powerful $\mathcal{H}$ IS NOT always good!
不能只追求在 training data 上能完全 fit ,而引進過高的模型複雜度導致 overfitting 。

Some Remark: VC bound 因為處理的情況很 general ,其是相當 LOOSE 的,實務上要達到夠小的 error rate ,不一定需要其所給出所需要的那麼多 data 量